Theorie: Eigenentwicklungen
Problemstellung

Nicht jedes praktisch relevante Optimierungsproblem lässt sich als LP, QP, … schreiben und mit bereits vorhandener Software lösen. Ist das Problem jedoch konvex oder ist das Ziel die Verbesserung einer bestehenden Lösung ohne Anspruch auf globale Optimalität, dann bestehen nichtsdestotrotz gute Chancen. Die Eigenentwicklung massgeschneiderter Algorithmen ist dann unentbehrlich
KKT Bedingung
Unter der Hypothese, dass sowohl die Zielfunktion \(f(x)\) als auch die Ungleichungen zweifach differenzierbar und konvex sind und die Gleichungen affin, ist die Lösung des Optimierungsproblemes
\begin{align} \min_x &~~~ f(x) \\ \text{s.t.}&~~~ (Ax)_k = b_k ~~~~~~~~~~~ k =1, … ‚m_1 \\ & ~~~ g_l(x) \le 0 ~~~~~~~~~~~~~ l=1, … ‚m_2 \end{align}
eindeutig definiert durch einen Satz Gleichungen. Diese heissen Karush-Kuhn-Tucker (KKT) Bedingungen und erklären, dass \(x^*, \lambda^*, \nu^*\) optimale primale und duale Optimierungsvariablen sind, wenn das Gleichungssystem
\begin{align} \nabla f (x^*) + \sum_{k=1}^{m_1} \nu_k^* \nabla (Ax^*)_k + \sum_{l=1}^{m_2}\lambda^*_l \nabla g_l(x^*) &=0 \\ (Ax^*)_k — b_k &=0 ~~~~~ k=1, …, m_1 \\ g_l(x^*) &\le 0 ~~~~~ l=1, …, m_2 \\ \lambda^*_l &\ge 0 ~~~~~ l=1, …, m_2 \\ \lambda^*_kg_l(x^*) &=0 ~~~~~ l=1, …, m_2 \end{align}
erfüllt ist [1, p. 244]. Die 5 Gleichungen reflektieren die Optimalitätsforderung gegenüber der Zielfunktion, die Zulässigkeit der primalen und dualen Variablen sowie eine Komplementaritätsbedingung, die duale Variablen und Nebenbedingungen koppelt.
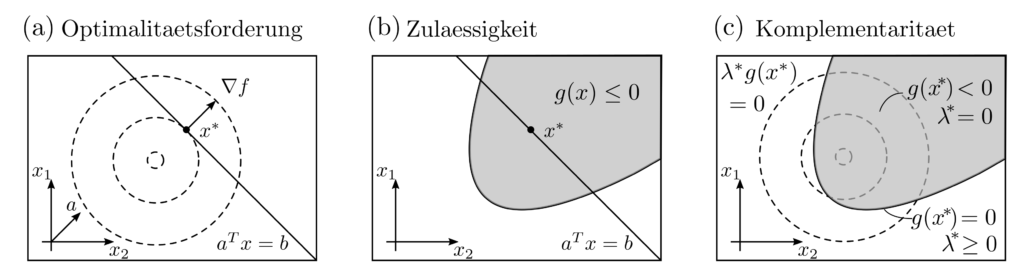
Newtonverfahren mit Nebenbedingungen
In dem KKT Gleichungssystem sind insbesondere die erste und dritte Zeile nichtlinear und eine direkte Lösung ist schwierig. Wie im Abschnitt zur Numerik beschrieben, können die Ungleichungen durch Barrierefunktionen ersetzt und die nichtlineare Gleichung mittels Newtonverfahren aufgelöst werden. Die Updates für die primalen und dualen Variablen
$$x_{k+1}=x_k + \Delta x ~~~~ \lambda_{k+1}= \lambda_k + \Delta \lambda ~~~~ \nu_{k+1}= \nu_k+\Delta \nu $$
ergeben sich aus einer Folge von Gleichungssystemen für die Suchrichtung \((\Delta x, \Delta \lambda, \Delta \nu)\). Die Gleichungssysteme sind indiziert von einer gegen \(0\) strebenden folge von Zahlen \(\mu_0, \mu_1, …\) und lauten [1, p. 610]
$$\begin{bmatrix} \Delta f (x_k) + \sum_{l=1}^{m_2}\lambda_l\Delta
g_l(x_k) & \nabla g(x_k) & A^T \\
-\operatorname{diag}(\lambda)\nabla g^T(x_k) &
-\operatorname{diag}(g(x_k)) & 0 \\ A & 0& 0\end{bmatrix}
\begin{bmatrix} \Delta x \\ \Delta \lambda \\ \Delta \nu \end{bmatrix} = — \begin{bmatrix} \nabla f(x_k) + \nabla g(x_k)+ A^T \nu \\ -\operatorname{diag}(\lambda) g(x_k) — \mu_k \vec{1} \\ Ax‑b \end{bmatrix} $$
wobei \(\vec{1}=[1, …, 1]^T\) , \( g(x_k)=[ g_1(x_k), … g_{m_2}(x_k)]^T\), \(\nabla g(x_k) ][\nabla g_1 (x_k), … ‚\nabla g_2(x_k)]\) mit \(\nabla g_l\) dem Gradienten von \(g_l\) und \(\Delta g_l(x_k))_{ij}=(\partial_{x_i} \partial_{x_j} g_l)(x_k)\). Der Term \( \operatorname{diag(v)}\) ist die matrix mit Einträgen des Vektors \(v\) auf der Diagonalen. Sinnvolle Verfahren zur Lösung der Gleichungssysteme führen zu Suchrichtungen \((\Delta x, \Delta \lambda, \Delta \nu)\) und letztendlich zur Lösung des mit dem KKT-System assizierten Optimierungsproblemes.
Numerische Stabilisierung
Das obige Gleichungssystem erweckt den Anschein, ein vollständiges und programmiertechnisch implementierbares Schema für konvexe Optimierung zu liefern. Dem ist nicht so. In der Praxis sind weitere Schritte durchzuführen, um numerische Stabilität zu gewährleisten. Dabei müssen Suchrichtungen unter anderem skaliert, zentriert, und korrigiert werden [2]. Andernfalls kann das Newtonverfahren konvergenzprobleme aufweisen. Bei Anwesenheit mehrerer lokaler Minima ist der Zusammenhang zwischen Startpunkt und Endpunkt des Newtonverfahrens zudem alles andere als offensichtlich. Siehe dazu auch die folgenden Illustrationen basierend auf Berechnungen von [3, p. 34] und [4, p. 21].
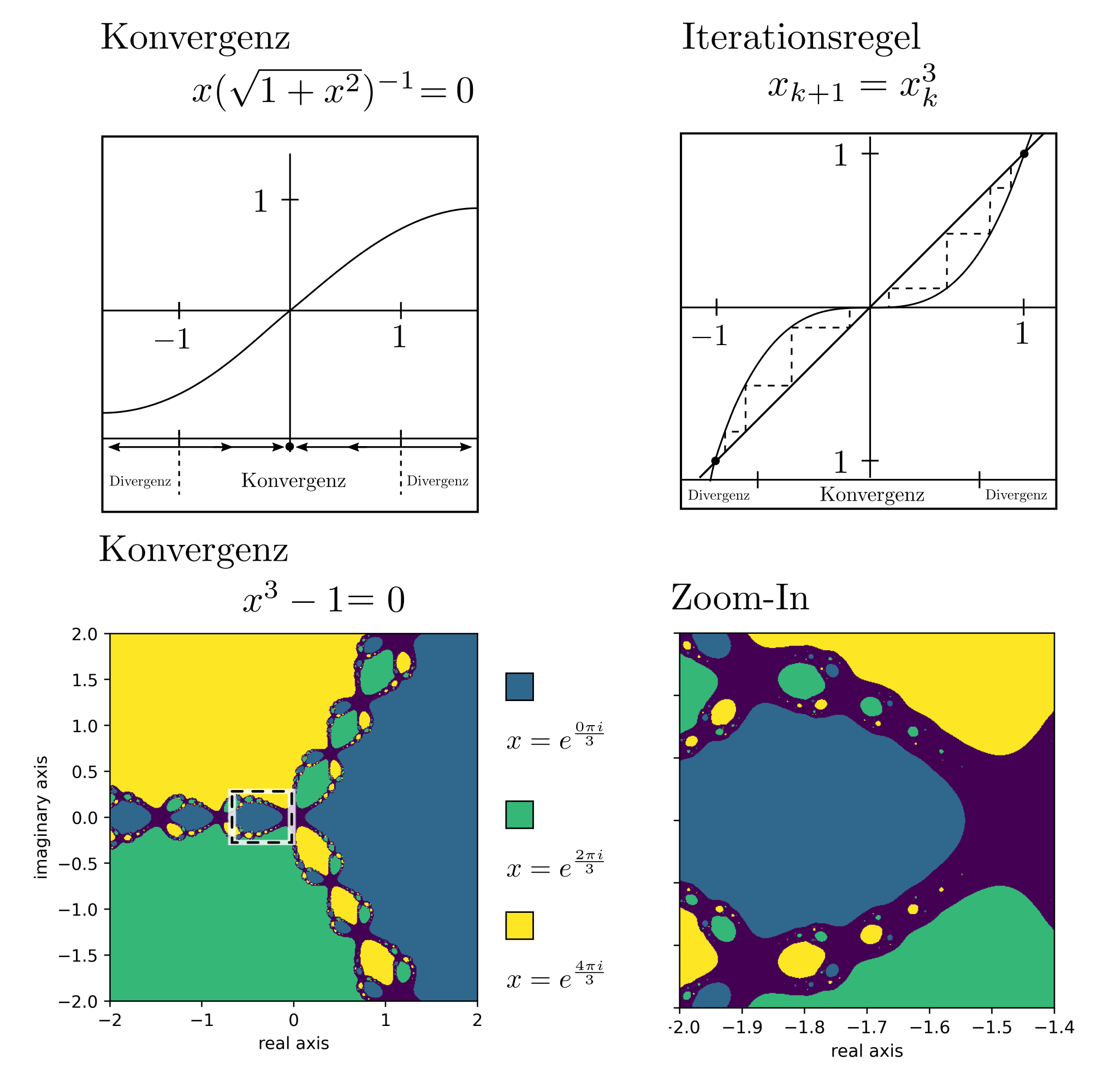
Beispiel
Die optimale Schätzung von Korrelationen in Daten ist essentiell für hochdimensionale Statistik im Zusammenhang mit stochastischen Prozessen. Sie kann als Maximierung der Wahrscheinlichkeit einer Wishart verteilten Zufallsgrösse aufgefasst werden, sodass letztendlich das Optimierungsproblem
\begin{align} \min_{\gamma} & ~~~ \log \det C_{\gamma} + \langle S, C_{\gamma}^{-1} \rangle_F + r\left[- \log \det \gamma + \langle \operatorname{diag}(\lambda) ^{-1}, \gamma \rangle_F\right] \\ \text{s.t.} & ~~~ A \gamma =b \\ & ~~~ \gamma \succeq 0\end{align}
entsteht [5, p. 193 ]. Dabei ist \(\gamma\) eine positive semidefinite Matrix von Optimierungsvariablen, \(\langle \cdot, \cdot\rangle_F\) das Frobenius-Skalarprodukt, \(S\) eine empirische Kovarianzmatrix, \(\lambda\) sind Eigenwerte und \(C_\gamma\) ist eine aus \(\gamma\) konstruierte Kovarianzmatrix und \(r\) ein Regularisierungskoeffizient. Die Newton-Schritte sind explizit berechenbar zu
\begin{align} \gamma_{k+1} =& \gamma_{k}+\Delta \gamma_{1}- \gamma A^T(A\gamma A^T)^{-1}A\Delta \gamma_1 \\ &\text{ mit } \Delta \gamma_1 = (1+r)^{-1}[(r‑1)\gamma +S_{\psi} — r\gamma \operatorname{diag}(\lambda)^{-1}\gamma] \\ & \text{ und } S_{\psi} \text{ einer transformierten Kovarianzmatrix} \end{align}
und die Optimierung kann z.B. in Python implementiert werden.
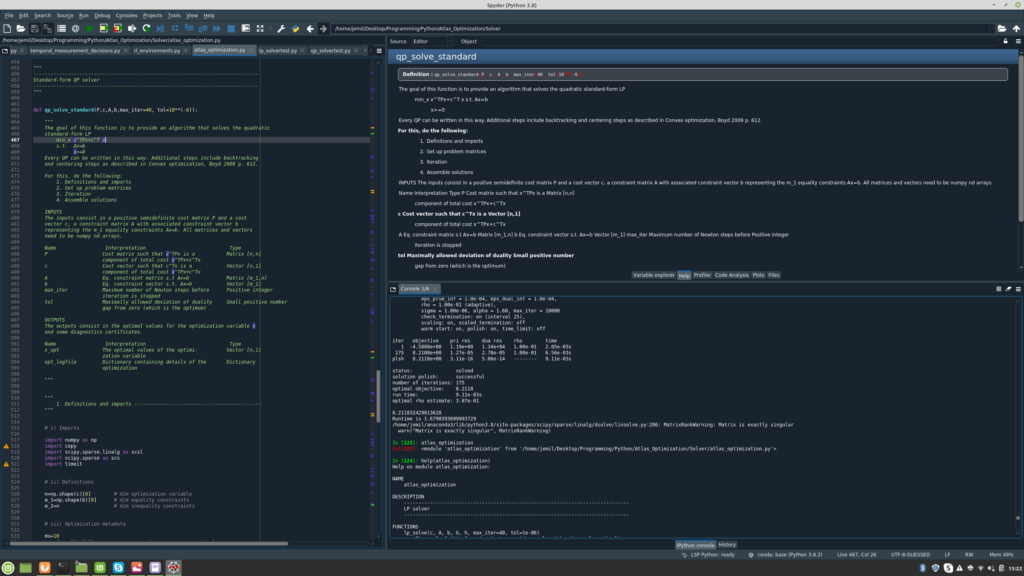
Implementation
Praktische Implementationen eines massgeschneiderten Optimierungsalgorithmus erfordern ein zuverlässiges Ökosystem numerischer Programme. Die Programmiersprache Python bietet mit NumPy [6] eine solche Umgebung an und zeichnet sich durch problemlose Interpretierbarkeit des Codes und die Verfügbarkeit einfach zu navigierender grafischer Benutzeroberflächen aus. Die Einstiegsfreundlichkeit ist sowohl für Entwickler als auch Kunden von Vorteil.
Code & Quellen
Beispielcode: Theory_newton_convergence.py in unserem Tutorialfolder
[1] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.
[2] Mehrotra, S. (1992). On the implementation of a primal-dual interior point method. SIAM Journal on Optimization. 2 (4): 575–601.
[3] Nesterov, Y. (2013). Introductory Lectures on Convex Optimization: A Basic Course. Berlin Heidelberg: Springer Science & Business Media.
[4] Sternberg, S. (2014). Dynamical Systems. New York: Courier Corporation.
[5] Butt, J.A. (2019). An RKHS approach to modelling and inference for spatiotemporal geodetic data with applications to terrestrial radar interferometry. Dissertation ETH Zürich, Zürich.
[6] Harris, C.R., Millman, K.J., van der Walt, S.J., Gommers, R., Virtanen, P., Cornapeau, D., Wieser, E., Taylor, J., Berg, S., Smith, N.J., Kern, R., Picus, M., Hoyer, S., van Kerkwijk, M.H., Brett, M., Haldane, A., Fernandez del Rio, J., Wiebe, M., Peterson, P., Gerard-Marchant, P., Sheppard, K., Reddy, T., Weckesser, W., Abbasi, H., Gohle, C., & Oliphant T.E. (2020). Array programming with NumPy. Nature, Vol 585, No. 7825.
