Optimal control - Atlas optimization

Optimal control: Übersicht

Definition

Unter dem Begriff optimal control sind Theorie und Methoden zur optimalen Steuerung von Systemen zusammengefasst; deutsche Namen für das feld sind unter anderem optimale Steuerung und Regelungstheorie. Steuerungssignale sind so zu wählen, dass ein bestimmter Systemzustand mit minimalem Kostenaufwand erreicht wird.

Die Systeme sind zwar auf entwicklungsgeschichtlichen Gründen oft physikalisch technischer Natur, können aber auch betriebswirtschaftliche, ökonomische, oder informationstechnische Prozesse abbilden,. Die Steuerungssignale sind dann z.B. dynamische Ressourcenflüsse, finanzpolitische Massnahmen, oder Speicherallokationsregeln. Gemeinsam ist allen Problemkonstellationen das Ziel, optimale Entscheidungen unter Unsicherheit zu treffen.

Optimal control unterscheidet sich von optimal estimation und optimal design durch die Anwesenheit einer Möglichkeit zur aktiven Steuerung des untersuchten Systems. Optimal control Probleme haben daher oft einen zeitlichen oder zumindest sequentiellen Aspekt, sodass Fragestellungen zur Dynamik des Systems und dessen Steuerbarkeit auftauchen.

Beispiel

Ein ferngesteuertes Auto soll in der Zeit $T$ von Position $x=0$ zu Position $x=1$ gefahren werden. Die Beschleunigung $\ddot{x}$ kann innerhalb bestimmter Grenzen durch das Steuersignal $u$ beeinflusst werden. Es soll über die gesamte Zeitdauer $T$ so gewählt werden, dass der Gesamtenergieverbrauch $\sum_{t=0}^T \ddot{x}_t^2$ minimal wird.

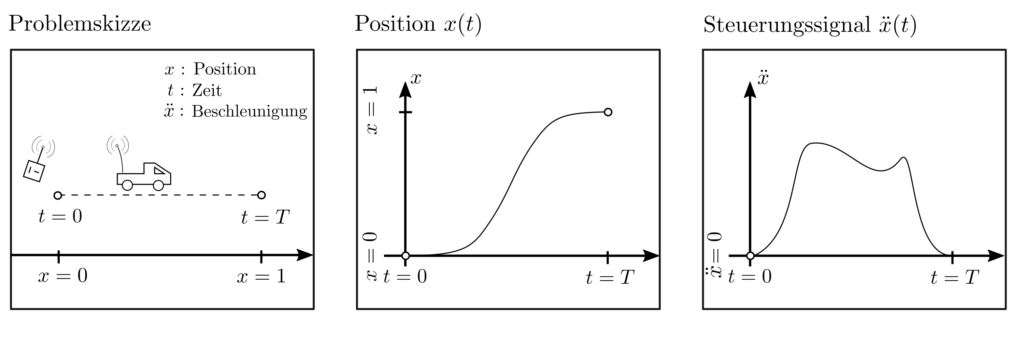
Das Optimierungsproblem hat die Form

$$ \begin{align} \min_{x_0, …, x_T, u_0, …, u_T} ~~~& \sum_{t=0}^T\ddot{x}_t \\ \text{s.t.} ~~~& x_{t+1}=Ax_t+Bu_t\\~~~&x_0=[0,0,0]^T ~~~~~~~~~ x_T=[1,0,0]^T \\ ~~~& A=\begin{bmatrix} 1 & \Delta t & 0 \\ 0 & 1 & \Delta t \\ 0 & 0 & 1\end{bmatrix} ~~~~ B=\begin{bmatrix} 0 \\ 0 \\ \Delta t \end{bmatrix} \end{align}$$

Problemklassen

Das obige Beispiel zeichnet sich durch einen hohen Grad an Planbarkeit aus und erfordert genaue Kenntnis über die dynamischen Zusammenhänge sowie eine Abwesenheit zufälliger Effekte. In der Praxis ist dies icht immer der fall, weswegen Formulierungen des optimal control Problemes auch für komplexere Situationen entwickelt wurden.

Statt eines vordefinierten Planes $u_0, …, u_T$ müssen dann aktuelle Beobachtungen des tatsächlichen Zustandes in die Steuerung miteingebunden werden und es entsteht ein Feedbackloop [2, p. 102]

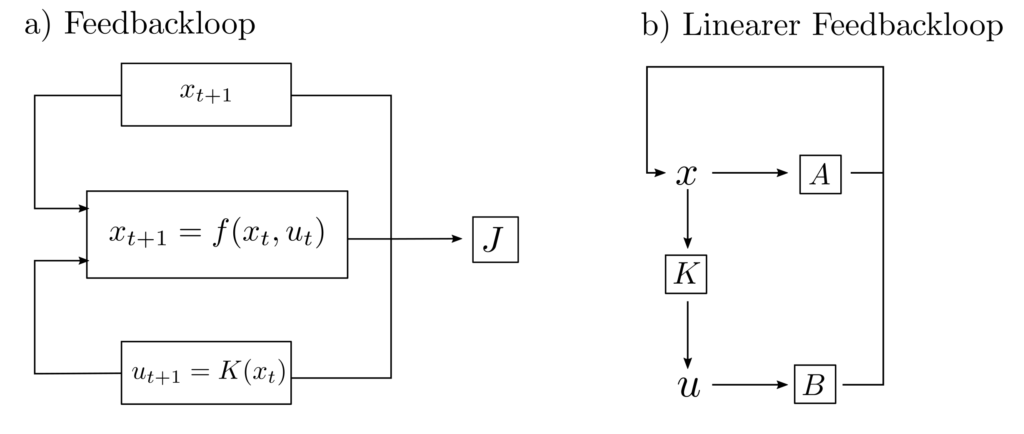
Es ist dann die Funktion $K(x_t)$ so zu finden, dass $J$ als Mass für die Unzulänglichkeit der Abfolge $f(x_0,u_0), …, f(x_T,u_T)$ minimal wird.

Klasse: Robustes optimal control

Robustes optimal control erweitert die Optimierung von Steuersignalen auf Situationen, in denen der Zusammenhang zwischen Szstemzuständen $x_t$, Steuergrössen $u_t$ und dem zeitlich nachfolgenden Systemzustand $x_{t+1}$ nicht vollständig bekannt ist.

Im obigen Beispiel entspräche das dem Fall, dass z.B. aufgrund von Schlupf oder Kraftübertragungsproblemen die Matrizen $A$ und $B$ teilweise unbekannte Elemente enthalten [1, p. 428].

Es muss dann ein Steuerungsinput $K(x_t)=u_t $ gefunden werden, welcher das System $$ x_{t+1}=Ax_t+Bu_t ~~~~~A\in \mathcal{A}, B\in \mathcal{B} $$

zufriedenstellend steuert unabhängig von den konkreten Matrizen $A\in \mathcal{A}$ und $B\in \mathcal{B}$. Dies läuft auf die simultane Erfüllung mehrerer linearer Matrixungleichungen hinaus und mündet in einem semidefiniten Programm.

Klasse: Stochastisches optimal control

Beim stochastischen optimal control wird die Systemevolution als zufallsbehaftet akzeptiert und statt direkt verfügbaren Systemzuständen $x_t$ sind nur verrauschte Beobachtungen zugänglich.

Wären z.B. im obigen Beispiel mit dem ferngesteuerten Vehikel zufällige unkontrollierbare Effekte wie etwa Wind oder Ungenauigkeiten in der Signalübertragung vorhanden, dann könnten die Systemzusammenhänge wie folgt beschrieben werden.

$$ \begin{align} x_{t+1}&=Ax_t+Bu_t+w\\ y_t&=Cx_t+v \end{align}$$

Dabei sind $x_t, A, B, u_t$ wie gehabt, $y_t=Cx_t$ sind die Beobachtungen der Zustände und $w$ und $v$ sind zufällige Grössen [1, p. 428], [3]. Sind überhaupt nur Zustandsänderungswahrscheinlichkeiten bekannt und womöglich Nichtlinearitäten vorhanden, dann können Markov-Entscheidungsprozesse zur Problemformulierung verwendet werden.

Klasse: Reinforcement learning

Sind weder dynamische Zusammenhänge noch Zustandsübergangswahrscheinlichkeiten bekannt, das zu steuernde System aber prinzipiell mittels eines Computermodelles simulierbar, dann kann Reinforcement learning eingesetzt werden.

Diese Situation entspräche im Zusammenhang des obigen Beispieles mit dem ferngesteuerten Auto die Situation, dass keinerlei apriori Informationen über das Verhalten von Systemzustand und Steuerungsinput vorhanden wäre.

Beim Reinforcement learning wird das Systemverhalten stattdessen empirisch untersucht, indem auf trial-and-error Basis Steuerungsvorschläge ausgeführt werden und deren Auswirkungen beobachtet. Dies führt zu einer Menge von Daten, die zum Training neuronaler Netze eingesetzt werden. Deren Aufgabe ist die nachbildung einer optimalen Funktion $u_t=K(x_t)$, die für jeden Zustand $x_t$ die beste Aktion $u_t$ vorschlägt.

Aufgrund des Einsatzes neuronaler Netze sind die Steuerungsinputs nichtlinearer natur und das Vorgehen ist sehr datenhungrig ohne dass Optimalität gewährleistet werden kann. Mittels dieses vorgehens sind jedoch Probleme lösbar, für die mit konventionellen Methoden keinerlei Hoffnung besteht. Beispiele dafür sind etwa das autonome Fahren oder die Entwicklung selbstlernender Algorithmen zur Bewegung von Robotern oder zur Steuerung von Computergegnern in Spielen [4].

Lösungen und Lösungsverfahren

Je nach Klasse der zu lösenden optimal control Problemes ist es trivial bis unmöglich zu lösen. Rein deterministische Planungsprobleme können oft durch Suchalgorithmen oder LP gelöst werden. Die Anwesenheit klar definierter zufälliger Effekte oder Modellunsicherheiten erfordert die Generierung stabilisierender Feedbackloops und die Minimierung von Fehlervarianzen, weshalb auf SDP zurückgegriffen werden muss. Sind überhaupt keine guten Prozessmodelle vorhanden, so können zur stochastischen Modellierung Markov-Entscheidungsprozesse eingesetzt werden oder es wird direkt Reinforcement learning verwendet.

Iterative Lösungsheuristiken und individuelle Untersuchungen der Lösungsvorschläge sind dann unvermeidbar. Die Methoden sind teilweise experimentell und definieren die Grenze des wissenschaftlich aktuell machbaren. Eine Lösung für ein optimal control Problem ist dann eine sogenannte Policy — eine Vorschrift für jede mögliche Situation, welches Verhalten optimal ist.

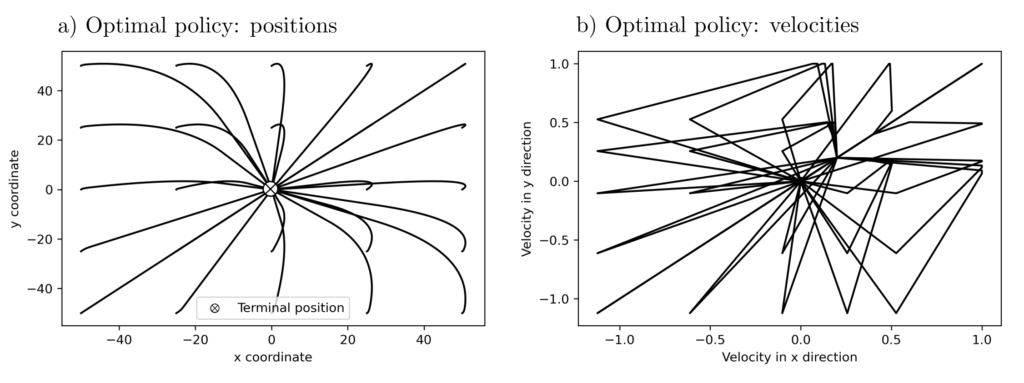
Abbildung 3 : 2‑dimensional Variante des Problemes zur Bewegungsplanung eines ferngesteuerten Vehikels. Dargestellt sind die $x,y$ Koordinatenwerte (a) und Geschwindigkeiten (b) benötigt zur energieeffizientesten Überführung eines beweglichen Objektes zum Mittelpunkt $\otimes$. Die verschiedenen Kurven korrespondieren mit verschiedenen Ausgangspositionen; die Initialbeschleunigung beträgt $[0.2, 0.2]$.

Anwendungen und praktisches

Für das optimal control gibt es unzählige Anwendungsmöglichkeiten. Sie umfassen technische Anwendungen wie die Regulierung chemischer Reaktionen, Roboterarmsteuerung oder die Koordination von Hafenkranarmen. Logistische Probleme wie etwa die adaptive Ampelsteuerung, adaptive Terminplanung von Überzeiten, Patiententerminen, Ambulanzeinsätzen, das Fahrzeugrouting und viele Probleme aus Produktionsplanung und Supply-chain management.

Der Übergang zuu finanziellen oder makroökonomischen Anwendungen wie etwa der Preisfestlegung von Finanzderivaten, dem aktien Portfoliomanagement und der Steuerung wirtschaftlicher Aktivitätsniveaus ist fliessend. Reinforcement learning gilt als praktisch anwendbare Methode der künstlichen Intelligenz. Mehr Beispiele sind hier zu finden.

In praktischer Hinsicht gibt es bei optimal control Problemen viele mögliche Fallstricke. Abseits von der Schwierigkeit, ein bestimmtes Ziel als konvexes Optimalitätskriterium zu formulieren, müssen z.B. Analysen durchgeführt werden, wie stabil die entwickelten Steuerungen sind gegenüber zufälligen Abweichungen. Ebenfalls ist nicht garantiert, dass ein angestrebter Zustand vermittels der zur Verfügung stehenden Steueroptionen überhaupt erreicht werden kann.

Code & Quellen

Beispielcode: OC_vehicle_control_1.py , OC_vehicle_control_2.py in unserem Tutorialfolder.

[1] Wolkowicz, H., Saigal, R., & Vandenberghe, L. (2012). Handbook of Semidefinite Programming: Theory, Algorithms, and Applications. Berlin Heidelberg: Springer Science & Business Media.

[2] Anderson, B. D. O., & Moore, J. B. (2007). Optimal Control: Linear Quadratic Methods. New York: Courier Corporation.

[3] Balakrishnan, V., & Vandenberghe, L. (2003). Semidefinite programming duality and linear time-invariant systems. IEEE Transactions on Automatic Control, 48,(1), 30–41.

[4] Vinyals, O., Babuschkin, I., Czarnecki, W.M. et al. (2019). Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature, 575, 350–254.