Optimal estimation: Parameterschätzung
Definition

Unter Parameterschätzung (auch Regression genannt) werden all diejenigen Aufaben zusammengefasst, die sich auf datengetriebene Modellanpassung zurückführen lassen. Dabei besteht das Ziel in der Wahl von Parametern, die das Modellverhalten in möglichst genaue Übereinstimmung mit tatsächlich beobachtetem Echtweltverhalten bringen.
Es spielt keine Rolle, welcher Natur die Daten sind und welche Komplexität das anzupassende Modell aufweist. Auch z.B. Bildklassifikation kann als Parameterschätzungproblem aufgefasst werden. Die Daten bestehen in dem Fall aus mit Bildklassen annotierten Bildern und das Modell ist ein neuronales Netz mit vielen Parametern, welches zu Bildern Bildklassen zuweisen soll. Die Übergänge zum maschinellen Lernen sind demnach fliessend.
Beispiel
Angenommen eine Wetterstation liefert in regelmässigen Abständen Temperaturmesswerte \(l_k, k=1, … ‚n\). Dies führt zu der Messreihe \( (l_1, z_1), … , (l_n, z_n)\) wobei mit \(z_k, k=1, … ‚n\) die Messzeitpunkte bezeichnet sind. In Erwartung langfristiger Trends und periodischer Schwankungen aufgrund tageszeitlich bedingter Einflüsse wird das folgende Modell \(g(x,z) \) zur Erklärung der tatsächlich beobachteten Temperaturmessdaten \(l\) vorgeschlagen:
$$ \begin{align} l \approx g(x,z) = & x_1g_1(z) + x_2 g_2(z) + x_3 g_3(z) \\ & \underbrace{x_1}_{\text{Konstante}} + \underbrace{x_2z}_{\text{linearer Trend}} + \underbrace{x_3\sin\left(\frac{2 \pi}{24}z \right)}_{\text{periodischer Einfluss}} \end{align}$$
In dem Modell sind die Parameter \(x_1, x_2, x_3\) unbestimmt und sollen so gewählt werden, dass \(g(x,z_k)\) und \(l_k\) ungefähr gleich sind.
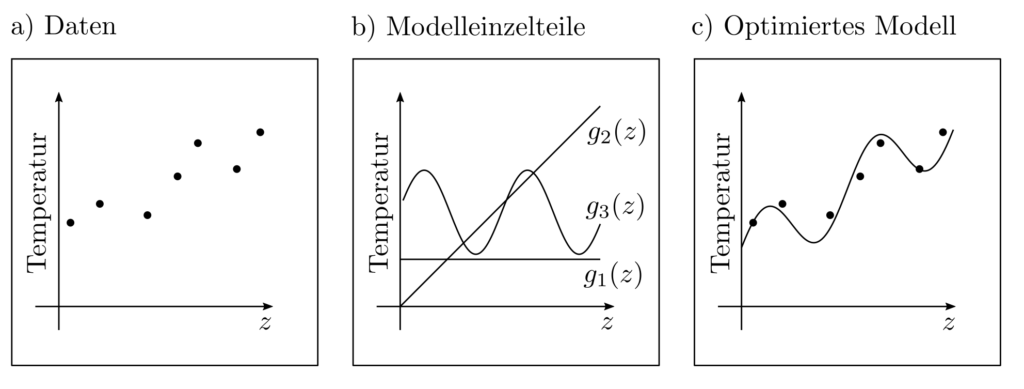
Die Lösung des Optimierungsproblemes
$$ \begin{align} \min_x ~~~& \sum_{k=1}^n (l_k‑g(x,z_k))^2 \end{align}$$
ist der optimale Parametervektor \(x^*=[x_1^*, x_2^*, x_3^*]^T\). Er lässt Interpretationen zu über die relative Stärke konstanter, linearer, und periodischer Effekte. Die Diskrepanz \(\sum_{k=1}^n(l_k‑g(x^*,z_k))^2\) ist ein Indikator für die Gesamteignung des Modellansatzes.
Generalisierung
Der obige Ansatz lässt sich problemlos auf Daten \(l_k\) beliebiger Dimension \(d_1\), Funktionsinputs \(z\) beliebiger Dimension \(d_2\), und beliebig viele Basisfunktionen \(g_1(x,z), … , g_m(x,z)\) ausdehnen. Das Optimierungsproblem zur Bestimmung der optimalen Parameter \(x^*\) lautet dann
$$ \begin{align} \min_x ~~~& \sum_{k=1}^n \|l_k-\sum_{j=1}^m x_jg_j(z_k)\|_2^2 \end{align}$$
wobei \(g(x,z)=\sum_{j=1}^m x_jg_j(z)\) eine Fubnktion von \(\mathbb{R}^{d_2}\) nach \(\mathbb{R}^{d_1}\) ist und \(\|v\|_2^2 = \sum_{k=1}^{d_1}v_k^2\) die Länge des Vektors \(v\in \mathbb{R}^{d_1}\) misst. In der obigen Form ohne weitere Nebenbedingungen oder Komplikationen handelt es sich um ein quadratisches Programm, dessen Lösung in expliziter Form aufgeschrieben werden kann als
$$ \begin{align} x &=(G^TG)^{-1}G^T l \\ l&\in \mathbb{R}^{n d_1} ~~~~ l=[l_{11}, … , l_{1 d_1}, …, l_{n1}, …, l_{nd_1}]^T \\ G & \in \mathbb{R}^{n d_1} \times \mathbb{R}^{m} ~~~~ G=\begin{bmatrix} G_1 \\ \vdots \\ G_n \end{bmatrix} \\ G_k &\in \mathbb{R}^{d_1} \times \mathbb{R}^{m} ~~~~ G_k=\begin{bmatrix} g_{11}(z_k) & \cdots & g_{n1}(z_k) \\ \vdots & \ddots & \vdots \\ g_{1d_1}(z_k) & \cdots & g_{md_1}\end{bmatrix} \end{align}$$
Hierbei ist \(g_{ij}(z_k)\) der \(j-\)te Eintrag des Vektors \(g_i(z_k\). Damit lassen sich Parameterschätzprobleme für z.B. zweidimensionale Trajektorien und Vektorfelder lösen; siehe Abbildung.
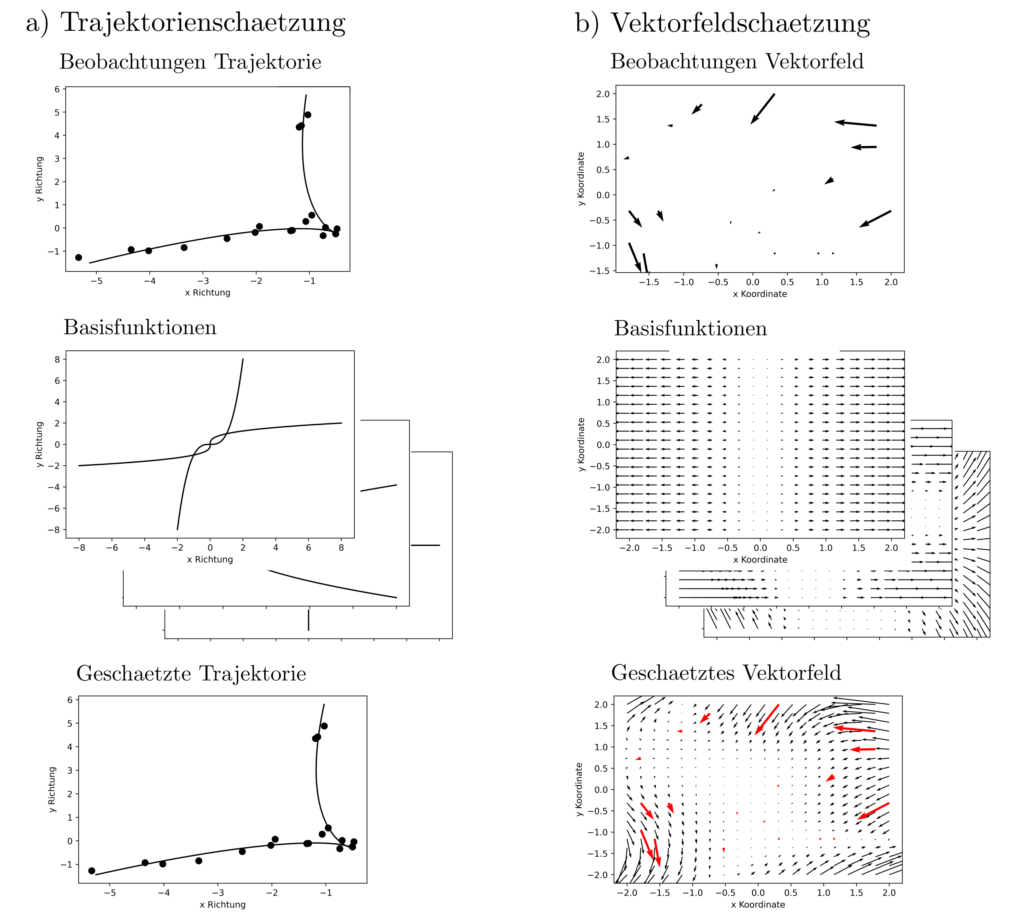
Interpretation
Die bisherigen Formulierungen beinhalten quadratische Zielfunktionen der Form \(sum_{k=1}^n \|l_k‑g(x,z_k)\|_2^2\) und sind demnach least-squares Probleme. Eine Minimierung dieser Zielfunktionen ist sinnvoll, wenn die Modellklasse \(g(x,z)=\sum_{k=1}^m x_mg_m(z) \) für irgendeine bestimmte Wahl von \(x\) die Daten vollständig erklären kann is auf (standard)normalverteile Residuen \(\epsilon\). Dann gilt
$$ l_k=g(x,z_k)+\epsilon_k \Leftrightarrow \epsilon_k= l_k‑g(x,z_k). $$
Die Wahrscheinlichkeiten der Residuen \(\epsilon_1, …, \epsilon_n\) sind dann \(p(\epsilon_k)= (2 \sqrt{\pi})^{-1} \exp\left( — \frac{1}{2} \epsilon_k^2\right)\). Die Wahrscheinlichkeit des Eintretens aller Residuen \(\epsilon_1, …, \epsilon_n\) gemeinsam ist
$$ p(\epsilon_1, …, \epsilon_n)=\prod_{k=1}^np(\epsilon_k) = (2^n \pi^{n/2})^{-1} \exp\left( -\frac{1}{2} \sum_{k=1}^n \epsilon_k^2 \right)$$ für statistisch unabhängige Residuen \(\epsilon_k \coprod \epsilon_j, k \neq j\). Eine wahl von \(x\) so, dass all die Residuen \(\epsilon_1= l_1‑g(x,z_1), …, \epsilon_n=l_n‑g(x,z_n)\) möglichst wahrscheinlich sind, führt auf
$$ \max_x p(\epsilon_1, …, \epsilon_n) \Leftrightarrow \min_x \sum_{k=1}^n \left(l_k‑g(x,z_k)\right)^2. $$
Die bisherigen Minimierungsprobleme lassen sich demnach schreiben als Wahrscheinichkeitsmaximierende Schätzer für den Erwartungswert von Daten \(l_k=g(x,z_k)+\epsilon_k\) unter der Annahme von unkorrelliertem, normalverteiltem Rauschen \(\epsilon_k\).
Alternativen zu least-squares
Nicht immer ist diese Annahme realistisch. Die Zielfunktion und Nebenbedingungen müssen gegebenenfalls angepasst werden, um die Eigenschaften der zugrundeliegenden, datengenerierenden Zusammenhänge angemessen zu reflektieren. So sind die beobachteten Daten eventuell statt stetiger Funktionswerte binäre Indikatorvariablen \(l\in \{0,1\}\), die den Ausfall eines Bauteiles anzeigen. Ist die Ausfallwahrscheinlichkeit als Funktion in Abhängigkeit von z.B. der Bauteileinsatzdauer abzuschätzen, dann führt dies auf die sogenannte logistische Regression [1, p. 119] zur direkten Schätzung der kumulativen Wahrscheinlichkeitsverteilung
$$p(\text{Bauteilausfall vor Zeit } t) = g(x,z)=[1+\exp(-x^Tz)]^{-1} $$
durch Maximierung der Gesamtwahrscheinlichkeit \(\prod_{k=1}^ng(x,z_k)^{l_k}(1‑g(x,z_k))^{(1‑l_k)}\) der Ausfallbeobachtungen \((l_1,z_1), … , (l_n,z_n)\). Auch mehrdimensionale erklärende Variablen wie etwa \(z=[\text{Einsatzdauer , Bauteilpreis}]\) sind erlaubt und ändern nichts an den Gleichungen.
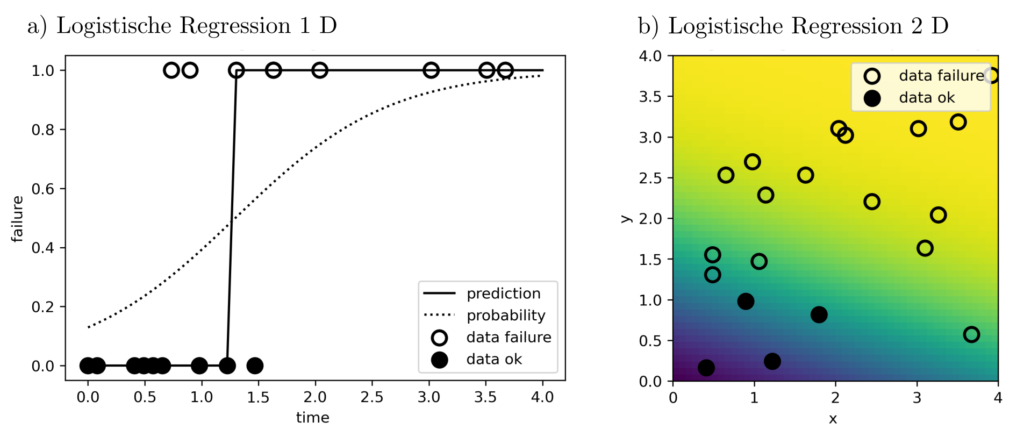
Anwendungen und Praktisches
Die klassische least-squares Parameterschätzung ist das Arbeitspferd der Datenanalyse und Modellierungsverfahren. Sie wird eingesetzt, wo auch immer Informationen aus daten zu extrahieren oder Modelle an reale Beobachtungen anzupassen sind. Sie ist leicht zu verstehen, gut erforscht, und erlaubt geschlossene und einfach zu implementierende Lösungsformeln. Sie ist daher enorm weit verbreitet und jegliche Aufzählung spezifischer Anwendungsmöglichkeiten wäre grob unrepräsentativ. Andere Parameterschätzungsansätze sind weniger weit verbreitet aber im Fall nciht normalverteilter Daten von essentieller Bedeutung.
Aus praktischer Sicht besteht die Schwierigkeit beim Formulieren von Parameterschätzungsproblemen häufig in der stochastischen Modellierung des Echtweltprozesses, der hinsichtlich seiner Wahrscheinlichkeitsverteilung analysiert werden soll. Sind zudem die Wahrscheinlichkeitsverteilungen nicht aus einer bestimmten parametrischen Familie, so sind die Wahrscheinlichkeitsmaximierenden Parameter unter Umständen nur schwierig zu finden, da das zugehörige Optimierungsproblem keiner der wohlbekannten Klassen LP, QP, SOCP, SDP angehört.
Code & Quellen
Beispielcode: OE_logistic_regression.py , OE_parameter_estimation_1.py , OE_parameter_estimation_2.py , OE_simulation_support_funs.py in unserem Tutorialfolder
[1] Hastie, T., Tibshirani, R., & Friedman, J. (2013). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Berlin Heidelberg: Springer Science & Business Media.
