Optimal estimation: Schätzung von Funktionen
Definition

Bei der Parameterschätzung werden vereinfachende Annahmen getroffen über den Ursprung beobachteter Daten \(l\). Sie gelten als erklärbar durch eine Funktion \(g(x,z)\), die abhängt von unter anderem Parametern \(x\).
Bei der allgemeinen Schätzung von Funktionen wird diese vereinfachende Annahme fallengelassen und die über Daten \(l\) beobachtete Funktion \(f\) nicht auf eine parametrische Familie beschränkt. Stattdessen wird \(f\) als stochastischer Prozess aufgefasst — als Menge von zu Orten \(t\in T\) zugeordneten und untereinander korrellierten Zufallsvariablen.
Relevanz
Durch diese stochastische Formulierung können Probleme formalisiert und gelöst werden, die der normalen Parameterschätzung nicht zugänglich sind. Zudem sind stochastische Prozesse ein flexibles Funktionsmodell für \(f\) und erlauben die Analyse von Daten für die kein überzeugendes parametrisches Modell der Form \(l=g(x,z)\) aus äusseren Umständen abgeleitet werden kann.
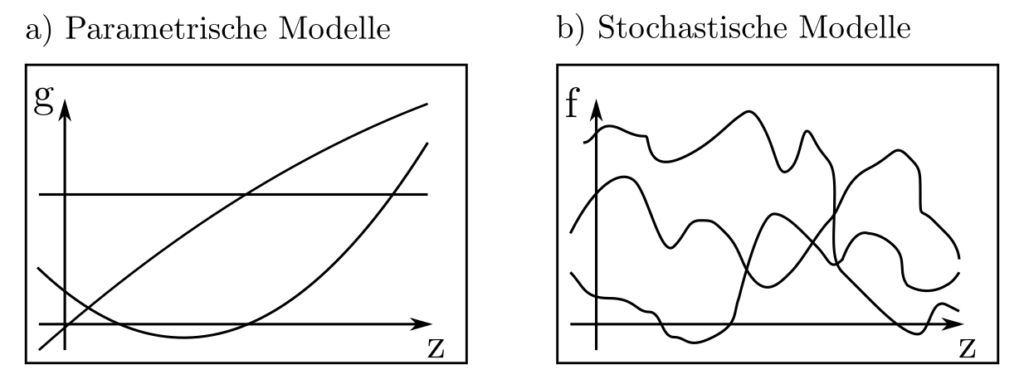
Typische Fragen
- Gegeben Messungen \(f(z_1), f(z_2)\), wie gross ist \(f\) an den anderen Stellen \(z\)?
- Wie hoch ist die Wahrscheinlichkeit, dass \(f(z_1)\ge 1\)?
- Gegeben Messungen \(f(z_1),f(z_2)\), wie gross ist \(\int_{0}^{1} f(z) dz\)?
- Sind die Daten erklärbar durch einen glatten oder einen unregelmässig-scharfkantigen Prozess?
Detailerklärung
Handelt es sich bei den Daten \(l_j, j=1, …, n\) beispielsweise um Messungen von Rohstoffvorkommen im Boden an den Orten \( z_j, j=1, …, n\), so sind die Fragestellungen allesamt wichtig zur Abschätzung wirtschaftlicher Rentabilität eines Rohstoffabbaus.
Tatsächlich wurde das Problem der Interpolation — Schätzung aller Funktionswerte \(f(z)\) auf Basis einzelner Messungen \(l_j=f(z_j), j=1, …, n\) — auch zuerst im Rahmen der Rohstoffprospektion systematisch untersucht [1]. Es gibt viele Funktionen \(f\) sodass \(l_j=f(z_j), j=1, …, n\) und so stellt sich die frage nach der gemäss Vorwissen und Daten wahrscheinlichsten Funktion \(f\).
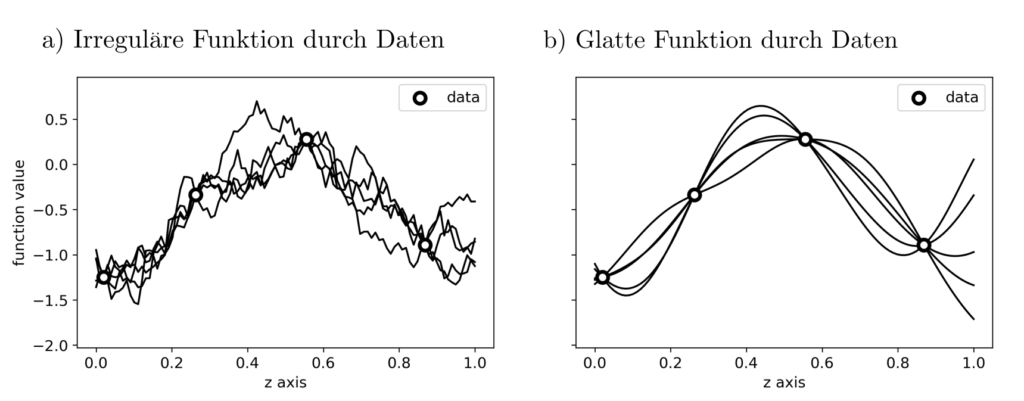
Interpolation: Optimierungsproblem
$$ \begin{align} \min_{f \in \mathcal{H}_K} ~~~& \|f\|_{\mathcal{H}_K}^2 \\ ~~~&\text{s.t.} f(z_j)=l_j ~~~~ j=1, …, n \end{align}$$
wobei \(\mathcal{H}_K\) ein Funktionsraum ist und \(-\|f\|^2_{\mathcal{H}_K}\) die Wahrscheinlichkeit einer Funktion \(f\) in diesem raum angibt. Details dieser Formulierung sind z.B. in [2, p. 111] zu finden; relevant ist vor allem die Umformulierung als quadratisches Programm zur Ermittlung von Gewichten \(\lambda \in \mathbb{R}^n\) mit \(f(z)=\sum_{j=1}^n\lambda_j l_j\).
$$ \begin{align} \min_{\lambda} ~~~& (1/2)\lambda^TK_{II}\lambda — \lambda^TK_{I} \\ \text{s.t.} ~~~\sum_{j=1}^n \lambda_j =1 \end{align}$$
\(K_{II}\) und \(K_{I}\) sind Matrizen und Vektoren beinhaltend die Korrelationsstrukturen von \(f\). Sie codieren die zugrundeliegenden Annahmen über z.B. die Glattheit von \(f\). Das Optimierungsproblem kann mit solvern für quadratic programming oder per Hand gelöst werden.
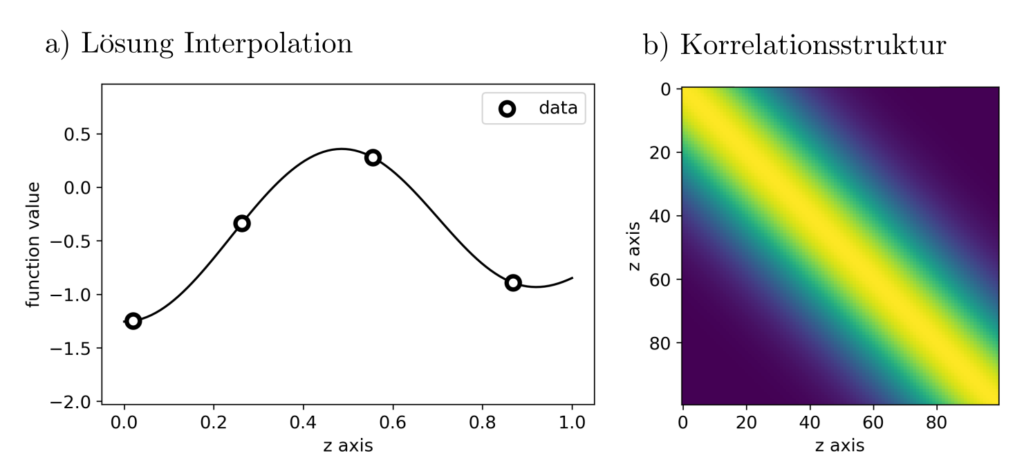
Korrelationsstruktur
Die Korrelationsmatrizen geben an, wie stark die Werte \(f(z_1), f(z_2)\) an unterschiedlichen Positionen \( (z_1, z_2)\) miteinander korreliert sind: Der Wert von \(0\) für \(z_1=0\) und \(z_2=1\) zeigt demnach an, dass zwischen \(f(0)\) und \(f(1)\) kein nennenswerter Zusammenhang besteht. Sind keine belastbaren Vorannahmen über die Korrelationsstrukturen möglich, dann kann sie auch aus den Daten abgeleitet werden. Dies ist ebenfalls ein optimales Schätzproblem und kann hier eingesehen werden.
Abstrakte Splines
Daten zu interpolieren ist of hilfreich. Nicht immer allerdings entstehen Daten aus punktuellen Messungen, sind fehlerfrei, oder hinsichtlich ihrer Korrelationsstruktur bekannt. Das momentan allgemeinste, immer noch effizient lösbare Schätzproblem lautet [2, p. 117]
$$ \begin{align} \min_f ~~~& \|Af‑l\|^2_{\mathcal{H}_A}+ \|Bf\|^2_{\mathcal{H}_B}& \\ &f : \text{ Gesuchte Funktion} && l : \text{ Daten} \\ & A : \text{ Messoperator} && \mathcal{H}_A : \text{ Funktionenraum potentieller Messungen} \\ & B : \text{ Energieoperator} && \mathcal{H}_B : \text{ Funktionenraum potentieller Energien} \end{align}$$
Lösungen für diese Minimierungsprobleme heissen abstrakte Splines und sie maximieren die Wahrscheinlichkeiten der Diskrepanzen \(Af‑l\) zwischen tatsächlichen und hypothethischen Beobachtungen sowie die Wahrscheinlichkeit von \(f\) selber. Der Messoperator \(A\) bildet Funktionen \(f\) auf hypothetische Beobachtungen \(Af\) ab und der Energieoperator \(B\) bildet Funktionen \(f\) ab auf Grössen \(Bf\), deren Wahrscheinlichkeitsverteilung bekannt ist.
Anwendungen
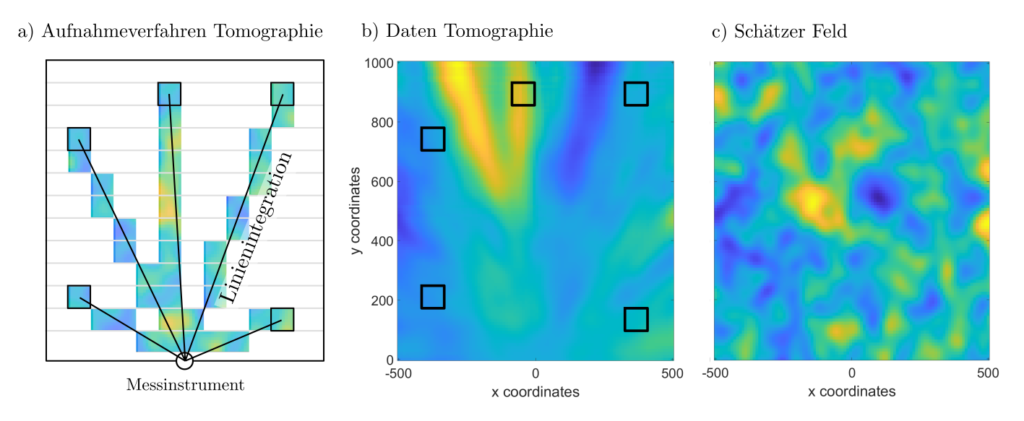
Die Lösungen enorm vieler optimal estimation Probleme lassen sich als abstrakte Splines darstellen. Ist etwa \(f\) eine zweidimensionale Funktion und \(Af\) sind Linienintegrale \( (Af)_j= \int_{z_0}^{z_j} f(z) dz\), dann handelt es sich bei den abstrakten Splines um Lösungen für Tomographieprobleme, siehe Abbildung.
Ist hingegen \(A\) einfach der Identitätsoperator und \(\mathcal{H}_A\) und \(\mathcal{H}_B\) sind Funktionenräume von Funktionen verschiedener Korrelationsstruktur, dann handelt es sich bei den abstrakten Splines um Lösungen für Signaltrennungsprobleme.
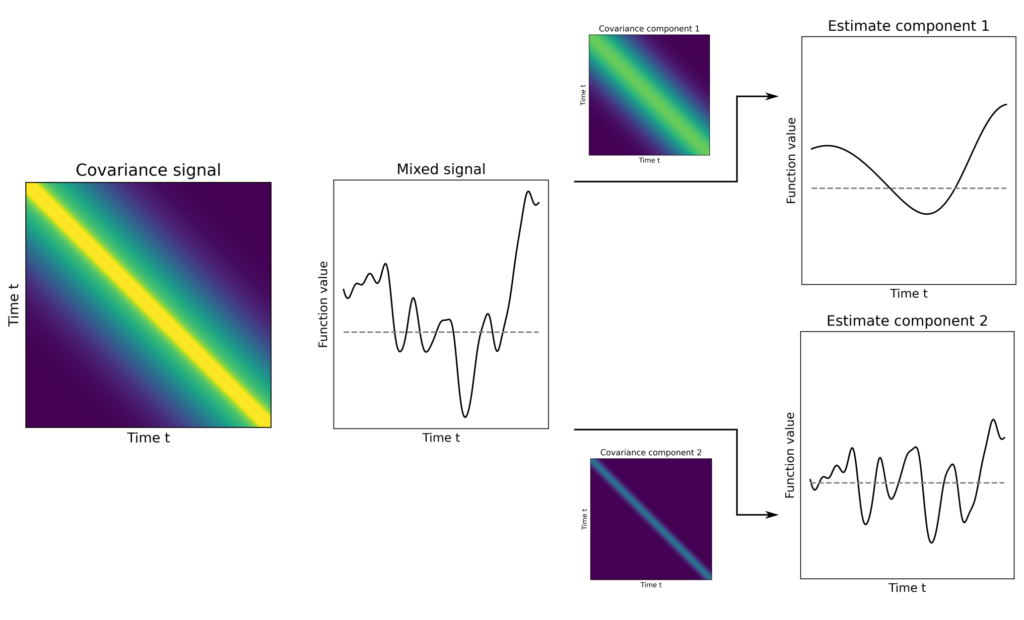
Neben diesen beiden Beispielen aus der Signalverarbeitung wir die optimale Schätzung von Funktionen auch für viele andere Zwecke eingesetzt. Anwendungen beinhalten die Rohstoffprospektion, Bildverarbeitung, Messdatenauswertung, die modellierung von Umweltphänomenen betreffend z.B. epidemiologische Ausbreitungsvorgänge, Verteilung von Atmosphärenparametern, geologische Eigenschaften, und Landnutzung sowie das Erstellen von Ersatzmodellen, das komprimieren und Filtern von Videodaten und vieles mehr.
Praktisches
Die Formulierung und Lösung von Echtwelproblemen als abstrakte Funktionsschätzungsprobleme beinhaltet verschiedene Schritte. An erster Stelle steht die herausforderung, eine bestimmte Aufgabe zu identifizieren als lösbar durch Schätzung einer Funktion. Dies ist nicht immer einfach. Weiterhin spielt die genaue Formulierung und umformung eine wichtige Rolle, um die Lösbarkeit des Optimierungsproblemes zu gewährleisten. Strikt gesehen handelt es sich bei abstrakten Splines nämlich um Optimierungsprobleme in unendlichdimensionalen Räumen (Funktionsräume haben diese Eigenschaft typischerweise); daher sind clevere manuelle Rechnungen erforderlich.
Zu guter letzt müssen die Korrelationsstrukturen der Lösungen entweder aus vorherigen Datengrundlagen oder auf Basis von Vorannahmen vorgeschrieben werden. Dies erfordert Erfahrungen in der Modellierung mit stochastischen Prozessen. Sind diese drei Herausforderungen erfolgreich gemeistert, so ist das Resultat der Bemühungen eine aus stochastischer Sicht optimale Schätzung.
Code & Quellen
Beispielcode: OE_conditional_simulation.py , OE_random_quantities.py , OE_functional_signal_separation.py , OE_simulation_support_funs.py in unserem Tutorialfolder
[1] Cressie, N. (1990). The origins of kriging. Mathematical geology, 22, 239–252.
[2] Berlinet, A., & Thomas-Agnan, C. (2011). Reproducing Kernel Hilbert Spaces in Probability and Statistics: . Berlin Heidelberg: Springer Science & Business Media.
