Optimal control: Planungsprobleme
Problemstellung
Ein System erhält in gewissem Rahmen frei zu wählende Steuerungsinputs und soll in einen vordefinierten Zustand gebracht werden oder eine bestimmte Verlaufstrajektorie nachvollziehen. In dieser völligen Generalität ist das Problem jedoch nur schwer zu handhaben.
Verkomplizierende Faktoren wie Nichtlinearitäten, unbekannte Systemdynamik, und Zufälligkeiten in den Wechselwirkungen zwischen Steuerungsinput und Systemreaktion können das Problem sogar zu einer komplett unlösbaren Angelegenheit werden lassen.
Im simpelsten Fall kompletter Vorhersagbarkeit des Systemes jedoch handelt es sich um ein statisches Planungsproblem und eine Lösung kann auf die Suche einer Sequenz von Steuerungsinputs reduziert werden. Diese Suche kann mit Hilfe dedizierter Suchalgorithmen wie der Monte-Carlo-Tree-Search durchgeführt werden oder sie wird als Optimierungsproblem formuliert, in welchem die Systemdynamik die Rolle von Nebenbedingungen einnimmt.
Mathematisches Modell
Hängt der Zustand x_{k+1} zum Zeitpunkt k+1 linear ab vom vorherigen Zustand x_k und dem Steuerungsinput u_k, so lässt sich die Systemdynamik schreiben als
x_{k+1}=Ax_k+Bu_k
wobei x_{k+1}, x_k \in \mathbb{R}^d, u_k\in \mathbb{R}^m typischerweise mehrdimensionale Vektoren sind. A und B sind Systemmatrizen, die den Einfluss von Zustand und Steuerungssignal auf den zukünftigen Zustand codieren. Soll das System so gesteuert werden, dass es einer Trajektorie f_1, …, f_n \in \mathbb{R}^d folgt bei möglichst kleinem Steuerungsinput, so kann das formuliert werden als das Optimierungsproblem
\begin{align} \min_{x_1, …, x_n, u_1, …, u_n} ~~~& \sum_{k=1}^n \|x_k-f_k\|_1+\|u_k\| \\ \text{s.t.} ~~~&x_{k+1}=Ax_k+Bu_k~~~ k=1, …, n \\ ~~~& x_1=x_{start} \end{align}
wobei x_1 als Startzustand x_{start} festgelegt sei. Die Optimierungsvariablen sind die n Steuerungsinputs u_1, …, n_n und die durch die dynamischen constraints beschränkten Zustände x_1, …, x_n. Es handelt sich um ein Optimierungsproblem mit nd+nm Variablen.
Es kann reformuliert werden als lineares Programm mit der Zielfunktion \|x‑f\|_1+\|u\|_1=\|v^{\Delta}\|_1+\|v^u\|_1 wobei x=[x_1^T, …, x_n^T]^T und u=[u_1^T, …, u_n^T]^T mit v^{\Delta} \in \mathbb{R}^{nd} und v^u\in \mathbb{R}^{nm} den Vektoren der Absolutbeträge der Elemente von x‑f und u.
\begin{align} \min_{x_1, …, x_n, u_1, …, u_n, v^{\Delta}, v^u} ~~~& \sum_{k=1}^n\sum_{l=1}^d v^{\Delta}_{kl}+ \sum_{k=1}^n \sum_{l=1}^m v^u_{kl} \\ \text{s.t.} ~~~&x_{k+1}=Ax_k+Bu_k~~~ k=1, …, n \\ ~~~& v^{\Delta} \ge x‑f ~~~ v^{\Delta}\ge -(x‑f) \\ ~~~& v^u\ge u ~~~~~~~~~~~ v^u \ge ‑u \end{align}
Die erste Ungleichung repräsentiert die Dynamik des Systemes während die letzten zwei Paare von die Positivität der Absolutresiduen v^{\Delta} und v^u sicherstellen [1, p. 294].
Beispiel: Antriebssteuerung
Eine Drohne sei so zu steuern, dass sie von ihrer jetzigen 3‑dimensionalen Position pos_1=[x_{start}, y_{start}, z_{start}] aus innerhalb von n Zeitschritten an der Zielposition pos_n=[x_{Ziel}, y_{Ziel}, z_{Ziel}] mit einer Gewschwindigkeit von v_n=[v^x_{Ziel}, v^y_{Ziel}, v^z_{Ziel}] eintrifft. Das (möglichst klein zu haltende) Steuerungssignal u wird direkt in Beschleunigung übersetzt, sodass der Zusammenhang
x_{k+1}= \begin{bmatrix} pos_{k+1} \\ v_{k+1} \\ a_{k+1}\end{bmatrix} = \underbrace{\begin{bmatrix} I & \Delta t I & 0 \\ 0 & I & \Delta tI \\ 0 & 0 & \Delta t I\end{bmatrix}}_{A} \underbrace{\begin{bmatrix} pos_k \\ v_k \\ a_k\end{bmatrix}}_{x_k}+\underbrace{\begin{bmatrix} 0 \\ 0 \\ \Delta t I \end{bmatrix}}_{B} \underbrace{\begin{bmatrix}u_x \\ u_y\\ u_z\end{bmatrix}}_{u_k}
gilt. Dabei ist I die 3 \times 3 Einheitsmatrix, \Delta t die Länge eines Zeitschrittes, pos steht für die Position, v für Geschwindigkeiten, und a für Beschleunigungen. Jeder Zustandsvektor weist demnach 9 Komponenten auf.
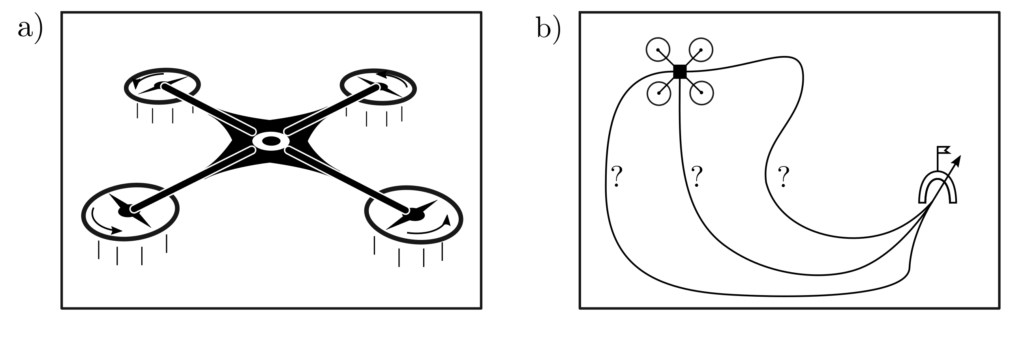
Lösung und Praktisches
Das zugehörige Optimierungsproblem ist
\begin{align} \min_{x_1, …, x_n, u_1, …, u_n} ~~~& \sum_{k=1}^n\|u_k\|_1 \\ \text{s.t.} ~~~&x_{k+1}=Ax_k+Bu_k~~~ k=1, …, n \\ ~~~& pos_1=[x_{Start}, y_{Start}, z_{Start}]^T ~~~~pos_n=[x_{Ziel}, y_{Ziel}, z_{Ziel}]^T \\~~~& v_1=[v^x_{Start}, v^y_{Start}, v^z_{Start}]^T ~~~~~~~~~~~~v_n=[v^x_{Ziel}, v^y_{Ziel}, v^z_{Ziel}]^T\\ ~~~& u_{min}\le u_k \le u_{max} ~~~k=1, …,n .\end{align}
Eine Illustration des Problemes bedindet sich in der nachfolgenden Abbildung. Man beachte, dass letztendliche Steuerungsinputs und Trajektorie signifikant von den Startbedingungen und möglichen Steuerungsinputbeschränkungen abhängen.
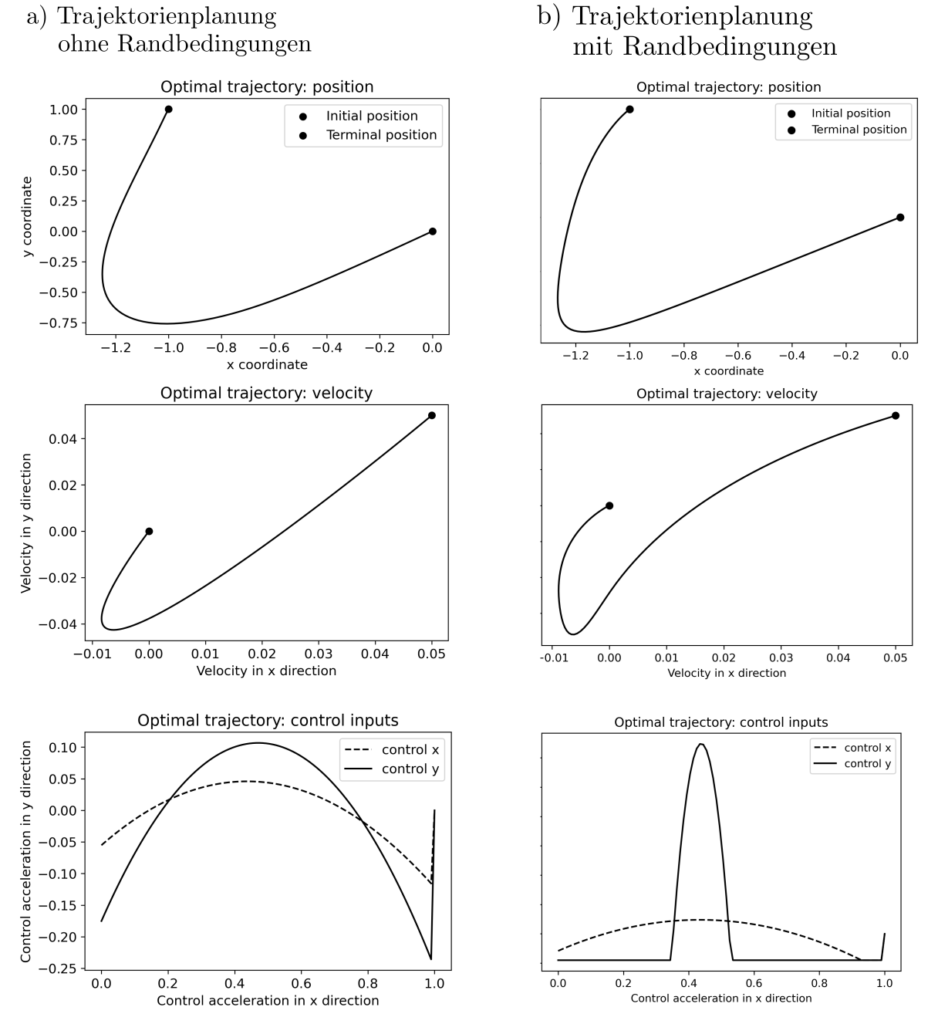
Das Problem wird mit hilfe der frei verfügbaren Software CVXOPT [2] und CVXPY [3] auf einem handelüblichen Laptop innerhalb weniger Millisekunden gelöst. Es existieren diverse Erweiterung. Die Zielfunktion enthält üblicherweise quadratische Terme und es ist möglich, Unsicherheiten in Systemdynamik und Umwelt durch zufällige Grössen zu Modellieren. Dies führt auf die linear-quadratisch Gausschen Zustandsregler (LQG) [4, pp. 164–207]. Um komplexe Optimierungen zu vermeiden wird häufig gefordert, dass u direkt als Funktion von x darstellbar sei mit u=Kx und einer konstanten Matrix K; siehe z.B. [5, pp. 421–441].
Code & Quellen
Beispielcode: OC_vehicle_control_3.py in unserem Tutorialfolder.
[1] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.
[2] Andersen, M. S., , Dahl, J., & Vandenberghe, L. (2022) . CVXOPT: A Python package for convex optimization, version 1.3
[3] Diamond S., & Boyd S., (2016). CVXPY: A Python-embedded modeling language for convex optimization. Journal of Machine Learning Research, 17(83), 1–5.
[4] Anderson, B. D. O., & Moore, J. B. (2007). Optimal Control: Linear Quadratic Methods. New York: Courier Corporation.
[5] Wolkowicz, H., Saigal, R., & Vandenberghe, L. (2012). Handbook of Semidefinite Programming: Theory, Algorithms, and Applications. Berlin Heidelberg: Springer Science & Business Media.
