Transport und Materialfluss - Atlas optimization

Optimal design: Transport und Materialfluss

Definition

Müssen Ressourcen auf verschiedene Orte verteilt werden und ist die Verteilung nur entlang bestimmter Wege möglich, dann spricht man von einem Tourenplanungsproblem. Dazu zählt auch das Design optimaler Flüsse von Gütern, Energie, oder Informationen durch komplizierte Netzwerke.

Dies sind Probleme, die besonders häufig im Transportsektor auftreten, wo sie sich äussern als Fragen nach den kürzesten Routen für Gütertransporte. Da gemäss z.B. der Studie [1] typischerweise bis zu 13 % der Gesamtherstellungskosten eines Produktes auf Transportkosten entfallen, ergeben sich hier enorme Einsparmöglichkeiten.

Ursprung Tourenplanung

Das sogenannte Travelling Salesperson Problem (TSP) ist ein archetypisches Tourenplanungsproblem, das schon im 19. Jahrhundert mathematische formuliert wurde. Beim TSP soll ein Händler eine Auswahl an Orten abfahren und dabei die Reihenfolge der Orte so wählen, dass die Gesamtdauer der Tour minimiert wird.

Das Problem wirkt trivial, ist aber nachgewiesenermassen eines der schwierigsten mathematischen Probleme. Zudem ist es unerwartet relevant auch ausserhalb des Transportwesens. Datenclustering, Verkabelung von Mikrochips, die Anordnung von Halbleiterkomponenten zu einem integrierten Schaltkreis, Flughafendesign, und die Steuerung grosser Teleskope zwecks Anzielung mehrerer Himmelskörper lassen sich allesamt in der Sprache der Tourenplanung formulieren. Siehe z.B. [2].

TSP: Beispiel

Das TSP ist ein Prototyp für viele Transport- und Ressourcenflussprobleme. Schon eine Instanz mit wenigen zu besuchenden Orten verdeutlicht die Schwierigkeiten. Es seien 4 Orte so zu besuchen, sodass die Reisezeit minimal wird. Wir verzichten der Einfachheit halber auf die Nebenbedingung, dass Startpunkt und Endpunkt identisch sein sollen.

Die kürzeste Tour im obigen Beispiel ist $1\rightarrow 2\rightarrow 3\rightarrow 4$ mit 10h Reisedauer. Dieses Resultat ist jedoch erst ersichtlich, nachdem alle $4!=4*3*2*1=24$ möglichen Touren durchgerechnet und deren Längen verglichen wurden. Dieses Verfahren basierend auf der Durchsicht aller möglichen Optionen verliert mit zunehmender Anzahl an Zielorten rapide an Praktikabilität. Für 12 Orte müssen bereits 500 000 000 Optionen durchgerechnet werden. Die Einführung von Nebenbedingungen und komplexeren Zielfunktionen erfordert einen komplett anderen Ansatz zur Lösung des Problemes.

Optimierungsformulierung

Die Formulierung von Tourenplanungsproblemen wie dem TSP ist mittels gemischt-ganzzahliger linearer Optimierung möglich. Dazu werden binäre Variablen $x_{ij}\in \{0,1\}$ eingeführt, die anzeigen, ob der Direktweg von Punkt $i$ nach Punkt $j$ zurückgelegt wird oder nicht. Mit $c_{ij}$ den Reisedauern zwischen den Punkten $i$ und $j$ ergibt sich das Optimierungsproblem [3]

$$\begin{align} \min{x_{ij}} ~~~ & \sum_{i=1}^n \sum_{j=1, j\neq i}^n c_{ij}x_{ij} &&\\ \text{s.t.} ~~~& \sum_{i=1, i \neq j}^n x_{ij}=1 &&j=1, …, n \\ &\sum_{j=1, j\neq i}^n x_{ij}=1 && j=1, …, n \\ & \sum_{i \in Q} \sum_{j\in Q, j\neq i} x_{ij}\le |Q|-1 && \forall Q\underset{\neq}{\subset} \{1, … , n\}, |Q|\ge 2 \end{align}$$

Die Rolle der Nebenbedingungen besteht im Erzwingen eines Flusses auf dem Transportnetz, bei dem jeder Ort genau einmal angefahren und auch verlassen wird und der keine Schleifen beinhaltet.

Generalisierung

Um der Komplexität fon Echtweltproblemen gerecht zu werden, erweisen sich in der Praxis weitere Nebenbedingugen und Modelldetails als nötig. So sind unter anderem folgende Sachverhalte zu modellieren:

Die Anwesenheit mehrerer Transportvehikel und die Möglichkeit zur Anmietung weiterer
Kapazitätsbeschränkungen der ausliefernden Vehikel
Maximale zulässige Fahrtdauern und fixe Zeitrahmen für Lieferungen
Gleichzeitiges Ausliefern und Produktrücknahmen
Vertragsstrafen bei nicht getätigten Lieferungen
Zufällige Effekte und robuste Tourenpläne

All dies sorgt dafür, dass Tourenplanungsprobleme oft sehr komplizierte mathematische Formulierungen haben mit einer unübersichtlichen menge an Gleichungen.

Beispiel

Es stehen 3 Vehikel zur Verfügung. Diese sollten eine Menge von $n=45$ Orten $v_i, i=1, … n$ so abfahren, dass die Länge der längsten Tour minimiert wird. Dies kann z.B. formuliert werden als das Optimierungsproblem [4, p. 154]

$$\begin{align} \min_{x_{ij}} ~~~& \max\big(\sum_{i<j} x_{ij}x_{ij}^1, && \sum_{i<j}c_{ij}x_{ij}^2, ~~~~~ \sum_{i<j} c_{ij}x_{ij}^3\big) \\ \text{s.t.} ~~~& x(\delta(\{v_0\}))=6 && \\ &x(\delta(\{v_i\})=2 && i=1, …, n \\ & x(\delta(S)) = 6 && S\subseteq V\setminus\{v_0\} \\ & 0 \le x_{0j}^k \le 2 && j=1, …, n ~~~ k=1, 2, 3 \\ & 0 \le x_{ij}^k \le 1 && i < j~~~ i,j =1, …, n ~~~ k=1, 2, 3 \\ & x_{ij}^k \in \mathbb{Z} && i\le j ~~~ i,j=1, …, n ~~~ k=1, 2, 3 \end{align} $$

Hierbei ist $x_{ij}^k$ eine Indikatorvariable, die anzeigt, ob das Vehikel $k$ von $i$ nach $j$ fährt, $V=\{v_0, …, n_n\}$ ist die Menge aller Orte inklusive des Start- und Endpunktes $v_0$ und $\delta(S)$ ist die Menge der Verbindungen aus der Menge $S$ hinaus. Der Term $x(\delta(S))$ ist die Summe der tatsächlich abgefahrenen Verbindungen aus der Menge $S$ hinaus.

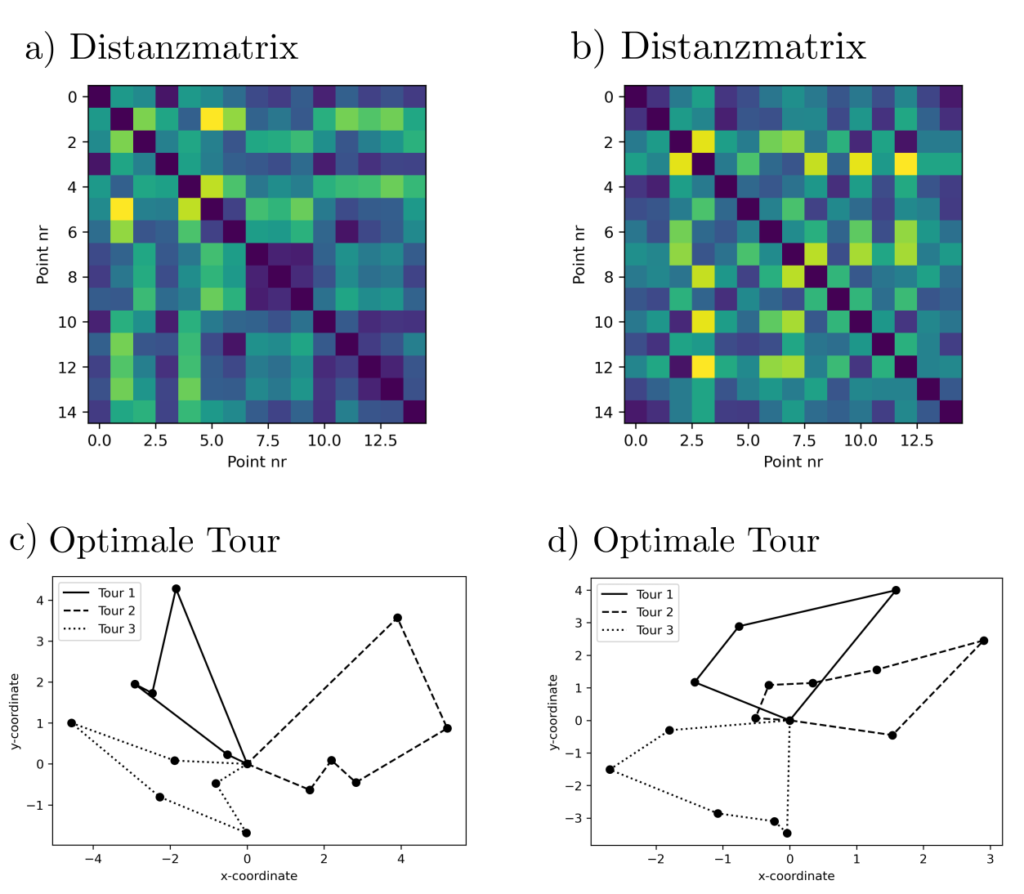
Lösung

Man beachte, dass die Forderung $x(\delta(S))=6 \forall S \subseteq V \setminus \{v_0\}$ eine Gleichung für jede Untermenge von $V=\{v_1, … ‚v_n\}$ beinhaltet. Da sind exponentiell viele Gleichungen und im obigen Beispiel ungefähr $2^{45}\approx 35$ Billionen. Diese sind weder per Hand formulierbar noch lösbar und auch für einen normalen Computer nicht zugänglich.

Es existiert jedoch leistungsfähige Software, die diese Probleme mittels Heuristiken approximativ löst. Wie haben für das obige Beispiel die Programmbibliothek OR-Tools von Google verwendet — eine Toolbox mit Python Interface, die sich explizit mit der Bereitstellung von Algorithmen für das Operations research beschäftigt. Mehr Informationen zu dem massgeblich von Laurent Perron und Vincent Furnon entwickelten und öffentlich verfügbaren Paket finden Sie hier .

Praktisches

Aufgrund der Schwierigkeit, Tourenplanungsprobleme exakt zu lösen, wurden Algorithmen entwickelt, die schnell zu guten aber vermutlich nicht optimalen Touren führen. Aufgrund der wirtschaftlichen Bedeutung von Transportproblemen ist viel Arbeit in die Entwicklung diverser Heuristiken geflossen und es sind einige praktische Regeln entstanden, die ohne grösseren Rechenaufwand ad-hoc von Anwendern benutzt werden können.

Ein Beispiel dafür ist die largest-gap-strategy, nach der GabelstaplerfahrerInnen ihre Routen in einem Warenlager wählen [5]. Tourenplanungsprobleme sind demnach noch immer nicht exakt lösbar aber zumindest approximativ. Und die durch Optimierung gefundenen Routen sind oft um 10–15% besser als manuell geplante [4, p. 153].

Code & Quellen

Beispielcode: OD_routing.py in unserem Tutorialfolder

[1] Owoc, M., & Sargious, M. A. (1992). The Role of Transportation in Free Trade Competition. In N. Waters (ed.), Canadian Transportation: Competing in a Global Context. Banff, Alberta, Canada.

[2] Lenstra, J. K. & Rinnooy, K. (1975). Some Simple Applications of the Travelling Salesman Problem. Operational Research Quarterly, 26(4), 717–733.

[3] Dantzig, G., Fulkerson, R., & Johnson, S. (1954). Solution of a large-scale Travelling Salesman Problem. Journal of the Operations Research Society of America, 2(4), 393–410.

[4] Appa, G. M., Pitsoulis, L., & Williams, H. P. (2006). Handbook on Modelling for Discrete Optimization. Berlin, Heidelberg: Springer.

[5] Petersen, C. G. (1997). An Evaluation of Order Picking Routing Policies. International Journal of Operations & Production Management, 17, 1096–1111.