Angebote: Lehrgänge
Überblick
Wir bieten mehrere halb- und ganztägige Lehrgänge an. Sie richten sich an generell Interessierte ohne Vorerfahrung (Optimierung I, Machine learning I) und an Personen, die regelmässig Kontakt mit mathematischer Modellierung haben und Ihre Fähigkeiten vertiefen wollen.
In den Vertiefungslehrgängen wird Material aus den Bereichen optimal estimation, optimal control, und deep learning behandelt. Sie liefern das Rüstzeug, konrekte Echtweltprobleme zu lösen.
Format
Wir legen Wert auf eine gesunde Mischung von Theorie und Praxis. Anwendungsorientierte Tutorials mit frei verfügbarer stat-of-the-art open source Software stehen ebenso auf dem Programm wie informelle Diskussionen, die Präsentation von grundlegender Theorie, Praxisbeispielen, neuen Erkenntnissen oder die Herleitung von Gleichungen. Die genaue Mischung dieser verschiedenen Elemente richtet sich nach den Lehrgangszielen und zum grossen Teil auch nach den Teilnehmenden.
Ihr persönlicher Mehrgewinn ist uns wichtig. In den Lehrgängen
- präsentieren wir Ihnen alles nötige zum Thema Optimierung und Machine learning
- diskutierenund implementieren Sie praxisnahe Beispiele an von uns bereitgestellten Laptops
- lernen Sie funktionierende Software kennen und nehmen sie mit nach Hause.
Lehrgänge
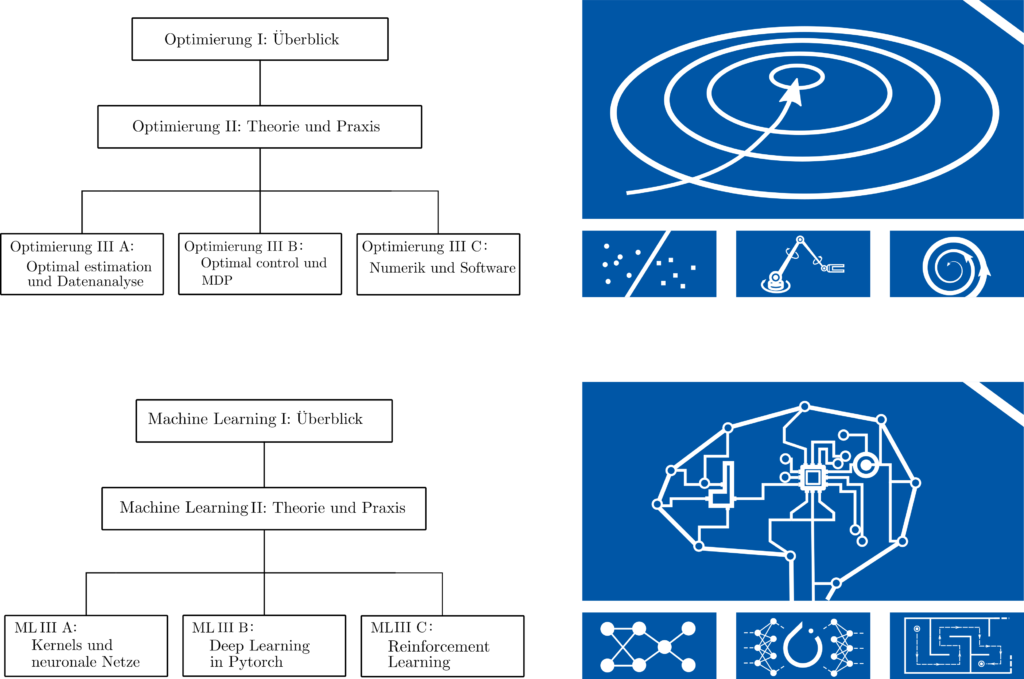
Detailbeschreibung
Grundlegende Informationen zu Theorien und Anwendungen von Optimierung und Machine learning finden Sie hier und hier. Haben wir Ihr Interesse geweckt oder benötigen Sie weitere informationen? Dann kontaktieren Sie uns und teilen Sie uns Ihre Fragen oder Anregungen mit. Die Lehrgangsteilnahme ist ab Frühling 2024 möglich; die Einschreibemöglichkeiten sind dann freigeschaltet.
| Lehrgang | Dauer | Schwierigkeit | Themen | ||
|---|---|---|---|---|---|
| Optimierung I: Überblick | 2 h | Definition Optimierung, Praktische Relevanz Optimierungsprobleme, Beispiele aus Natur, Technik, Wirtschaft, Lösbarkeit von Optimierungsproblemen, Stand der Technik, Forschungsrichtungen, Praktisches. | |||
| Optimierung II: Theorie und Praxis | 4 h | Mathematische Formulierung von Optimierungsproblemen, lineare, quadratische, second order cone, semidefinite, stochastische, und dynamische Programmierung, Einsatzbereiche, Beispielprobleme, Modellierungstechniken, Python und CVXPY | |||
| Optimierung III A: Optimal estimation und Datenanalyse | 6 h | Stochastische Modelle, Least squares, Parameterschätzung, Interpolation und Glättung von hochdimensionalen Daten, Hilberträume, Indirekte Beobachtungen, Worst Case Wahrscheinlichkeitsabschätzungen | |||
| Optimierung III B: Optimal control und Markov decision processes | 6 h | Systemanalyse, Systemidentifikation, Stabilität, Steuerbarkeit und Observabilität, Linear quadratische Regler, Robustes optimal control, stochastisches optimal control, Lineare Matrixungleichungen und semidefinite Programmierung, Markov Entscheidungsprozesse, State of the Art, Beispielanwendugnen | |||
| Optimierung III C: Numerik und Software | 4 h | Naive Verfahren, Konvexität, Newton Verfahren, Interior point methods, Dualität, Standardformulierungen, LP und QP solver selbst programmieren, VCXPY, Formulieren von Problemen in CVXPY, Interpretation von outputs, state-of-the-art open source und kommerzielle solver | |||
| ML I: Überblick | 2 h | Definition und Abgrenzung machine learning, Überblick, Erfolgsgeschichten, Supervised, Unsupervised, Reinforcement learning, Anwendungsbeispiele, Fail cases, Optimierungsformulierungen und Lösungen, Was kann man mit ML lösen? | |||
| ML II: Theorie und Praxis | 4 h | ML als statistisches Optimierungsproblem, simple Beispiele, die klassischen 5 Aufgaben, Beispiele und Python libraries, neuronale Netze, Training und Test, Architektur ML software und packages | |||
| ML III A: Kernels und neuronale Netze | 6 h | Unendlichdimensionale Räume und kernels, Features und Featuredesign, nichtlineare features, support vector machines, RKHS und der kernel Trick, ANN’s als universelle Funktionsapproximatoren, Architektur und Training, Konvergenz, Layerinterpretationen, Anwendungen wie z.B. neural style transfer | |||
| ML III B: Deep learning mit PyTorch | 6 h | Manuelle features vs deep learning, Lernen aus Bildern, Netzarchitektur, Erkennung Postleitzahlen in Bildern, SVM’s vs DL, Nichtkonvexität, Konvergenzprobleme, ADMM, Praktische Umsetzung in PyTorch, Blick in ein ANN, Imagenet, Netzarchitekturen für Text, Bild‑, Zeitreihendaten | |||
| ML III C: Reinforcement learning | 6 h | Grenzen klassischer optimal control Formulierungen, Belohnungsformalismus, Reinforcement learning Paradigmen, biologische Grundlagen, Markov Entscheidungsprozesse, Policies als Lösung, stochastische Transitionsmodelle, Exploration vs Exploitation, Aktuelle Erfolge und Algorithmen, Umsetzung in Stable Baselines3, Beispielanwendungen | |||
Programmiersprache
In den Lehrgängen verwenden wir die Programmiersprache Python und die open source frameworks CVXOPT, CVXPY, PyTorch, und Stable Baselines3 sowie die von uns entworfene Atlas optimization suite. Optimierungs- und Machine learning Probleme können mit Hilfe dieser Softwarepakete über eine graphische Benutzeroberfläche formuliert und gelöst werden, ohne sich mit programmiertechnischen Details herumzuärgern.
Die vertiefenden Kurse eignen sich daher auch für Personen ohne Programmierkenntnisse. Sie benötigen allerdings etwas Erfahrung im Umgang mit mathematischen Methoden. Die Kurse finden in Zürich oder auf Firmenwunsch hin auch ausserhalb statt.
