Reinforcement learning - Atlas optimization

Optimal control: Reinforcement learning

Definition

Reinforcement learning (RL) ist eine Methode für das optimal control unter sehr herausfordernden Bedingungen. Die Zustandsänderungen sind zufällig, die Wahrscheinlichkeiten nicht bekannt und die zu optimierende Funktion selber verfügt über keine geschlossene Form. Dennoch soll eine optimale policy gefunden werden.

Unter einer policy versteht man einen Plan, der für jeden möglichen Zustand dasjenige Steuersignal angibt, welches über lange Sicht zu den besten Ergebnissen führt. Das derartig formulierbare Aufgabenspektrum ist so allgemein, dass von der Maschinensteuerung über die adaptive Planung von Search-and-Rescue Missionen bis hin zur Entwcklung von eigenständig lernenden und auf Weltmeisterniveau spielenden Schachalgorithmen alls als RL Problem aufgefasst werden kann.

Beispiel

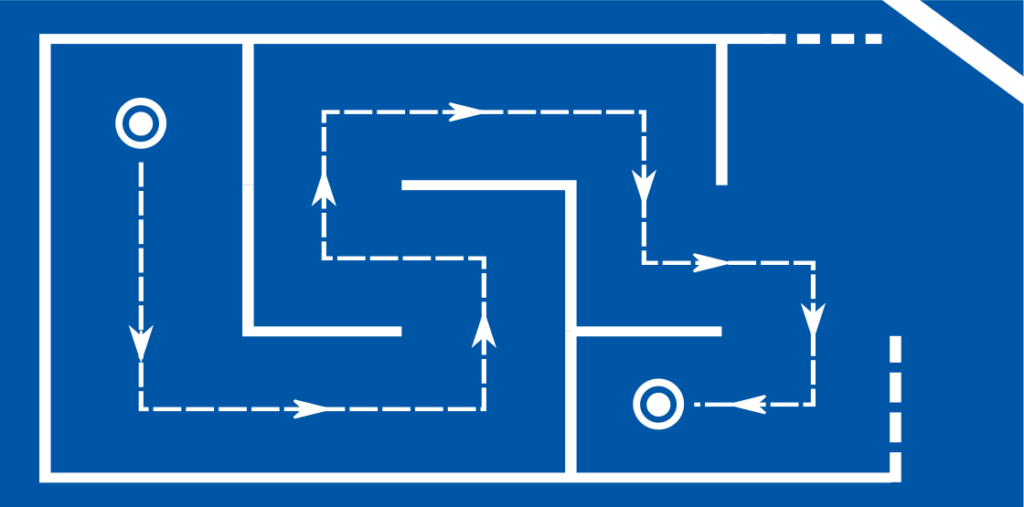
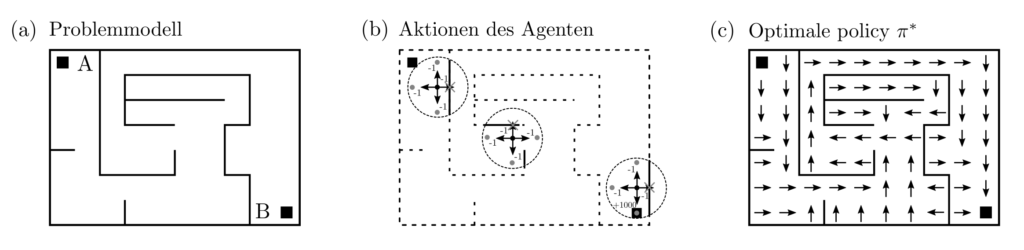
Ein beispiel für ein instruktiv mit RL lösbares optimal control Problem ist die navigation eines Labyrinthes vom Startpunkt $A$ bis zum Zielpunkt $B$. Das Layout des Labyrinthes sei unbekannt aber vom das Labyrinth navigierenden Algorithmus lokal abfragbar. Da der Algorithmus mit seiner Umgebung zwecks Informationsgewinnung aktiv interagieren kann, wird er auch Agent genannt. Das obige Problem als LP, QP, … SDP zu beschreiben wäre ‑falls überhaupt möglich — enorm schwierig.

Beispielanalyse

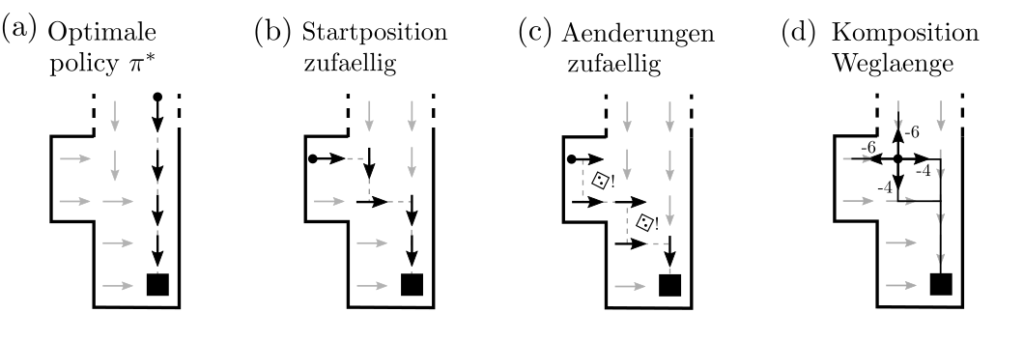
Die Lösung des Labyrinthproblemes ist eien Policy $\pi^*:S\ni s\mapsto \pi^*(s)\in A$, welche eine Position $s\in S$ als Input akzeptiert und als Output eine Aktion $a\in A$ generiert. Es wird damit nicht nur ein starrer Plan von Positionen $s_A, s_1, …, s_B$ vorgeschlagen, sondern das Planungsproblem für alle möglichen Anfangspositionen gleichzeitig gelöst. Wäre der Agent nun auf eine beliebige Position $s_0$ gesetzt, und soll von dort auf den kürzesten Weg zu $B$ finden, so gelingt ihm auch das durch Befolgung der Policy $$s_0\stackrel{\pi^*(s_0)=a_0}{\rightarrow} s_1\stackrel{\pi^*(s_1)=a_1}{\rightarrow} …\stackrel{\pi^*(s_n)=a_n}{\rightarrow}s_B .$$ Selbiges gilt, wenn die Positionsänderungen vom zufall beeinflusst werden und die genaue Folgeposition nicht zu 100% aus den vergangenen Positionen und der gewählten Aktion folgt.

Abbildung 2: Die Policy $\pi^*$ weist den kürzesten Weg von $A$ nach $B$ (a).Auch für andere Startpositionen und in der Gegenwart von Zufallseffekten erfüllt sie diese Rolle (b), ©. Jedem Paar von Position $s_0$ und Aktion $a$ kann die noch erreichbare kürzeste Weglänge zugewiesen werden und diese Funktion erfüllt eine Kompositionseigenschaft: Der Wert von $(s_0,a)$ ist die Weglänge von $s_0$ nach $s(s_0,a)$ plus die kürzeste Weglänge von $s(a_0,a)$ nach $B$ (d).

Formulierung von RL Problemen

RL Probleme werden ähnlich formalisiert wie Markov decision processes. Als Input für RL Algorithmen wird ein Computermodell benötigt, dass

Den Zustandsraum $S$ und den Aktionsraum $A$ definiert
Für jedes Paar $(s,a)\in S\times A$ eine (stochastische) Belohnung $r(s,a)$ generiert
Für jedes Paar $(s,a)\in S \times A$ (stochastisch) einen Nachfolgezustand $s’(s,a)$ generiert.

Diese Anforderungen sind noch etwas schwächer und praktisch gesehen einfacher zu handhaben als bei Markov decision processes. Statt einer tabellarischen ganzheitlichen Erfassung der Belohnungen $r(s,a)$ und Übergangswahrscheinlichkeiten $p(s’|s,a)$ zwischen Zuständen benötigt RL lediglich Beispiele. Das Ziel ist die Ermittlung einer optimalen Policy $\pi^*$, welche den Erwartungswert der kumulativen belohnungen maximiert.

$$ \begin{align} \max_{\pi} ~~~&E_{\pi}\left[ \sum_{k=1}^{\text{End}} r(s_k,a_k)\right] \\ s.t. & a_k=\pi(s_k)\end{align}$$

Dabei denotiert $E_{\pi} \left[\sum_{k=1}^{\text{End}}r(s_k,a_k)\right]=\eta(\pi)$ den Erwartungswert der kumulativen Belohnungen, wenn Policy $\pi$ verfolgt wird.

Lösung

Es gibt verschiedene Ansätze zur Ermittlung von $\pi^*$. Ihnen gemeinsam ist, dass der Agent Daten durch Interaktion mit dem Computermodell sammelt nd die Erfahrungen über Zustände, Aktionen, Zustandsänderungen, und Belohnungen in ein Feedbackloop zur Ermittlung von $\pi^*$ einfliessen lässt.

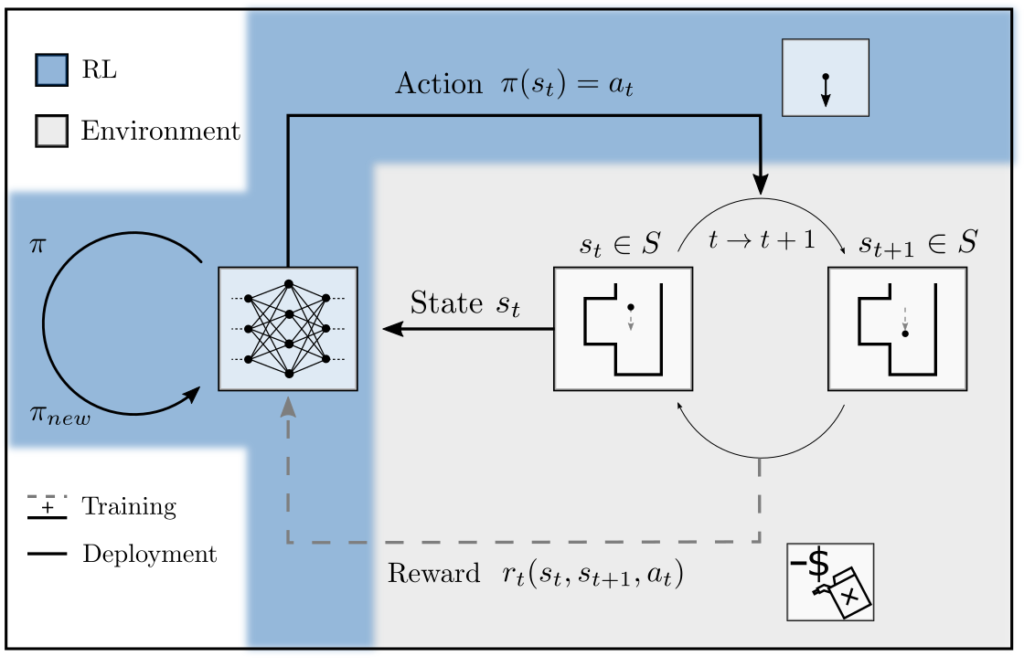
Die Funktion $\pi:A\rightarrow S$ wird aus Flexibilitätsgründen oft als neuronales Netz $\pi_{\theta}$ konstruiert. Es kann dann auf Basis der Daten angepasst werden, indem z.B. die Ableitungen von $\eta(\pi)$ nach den Parametern $\theta$ von $\pi$ gebildet werden [1, p. 367].

$$\begin{align} \eta(\pi) & =\int_{(S\times A)^n} \sum_{k=0}^nr(s_k,a_k)p_{\theta}(\xi)d\xi \\ \nabla_{\theta} \eta &= \int_{(S\times A)^n}\sum_{k=0}^n r(s_k,a_k) \nabla_{\theta}\left[ \log p_{\theta}(\xi)\right] p_{\theta}(\xi)d\xi \\ \hat{\nabla}_{\theta} \eta & = \frac{1}{m}\sum_{j=1}^m \left( \sum_{k=0}^n r(s_k^j,a_k^j)\right)\nabla_{\theta}\left[ \log p_{\theta}(\xi)\right] \\ & =\frac{1}{m} \sum_{j=1}^m \left( \sum_{k=0}^n r(s_k^j,a_k^j)\right)\sum_{k=0}^n\nabla_{\theta}\log \pi_{\theta}(s_k^j,a_k^j)\end{align}$$

Dabei ist $p_{\theta}(\xi)$ die Eintrittswahrscheinlichkeit der Sequenz $[(s_0,a_0), …, (s_n,a_n)]$ und $\hat{\nabla}_{\theta} \eta$ ein datengetriebener Schätzer für den Gradienten der kumulativen Belohnung. Die obigen Gleichungen werden z.B. im Algorithmus TD3 [2] verwendet und sind in der Python Bibliothek Stable Baselines3 [3] implementiert.

Beispiel: Landungsvorgang

Der Landevorgang eines Objektes ist so zu steuern, dass es an der designierten Koordinate $0$ auftrifft. Der Landevorgang folgt den üblichen Differentialgleichunegn, die Position, Geschwindigkeit, und Beschleunigung koppeln, doch das ist dem Algorithmus nicht bekannt. Beim Auftreffen auf den Boden nach der Zeit $T$ wird eine Belohnung von $-|x(T)|$ ausgeschüttet, die die Abweichung von tatsächlichem und designiertem Landepunkt bestraft und so als zu minimierend festlegt.

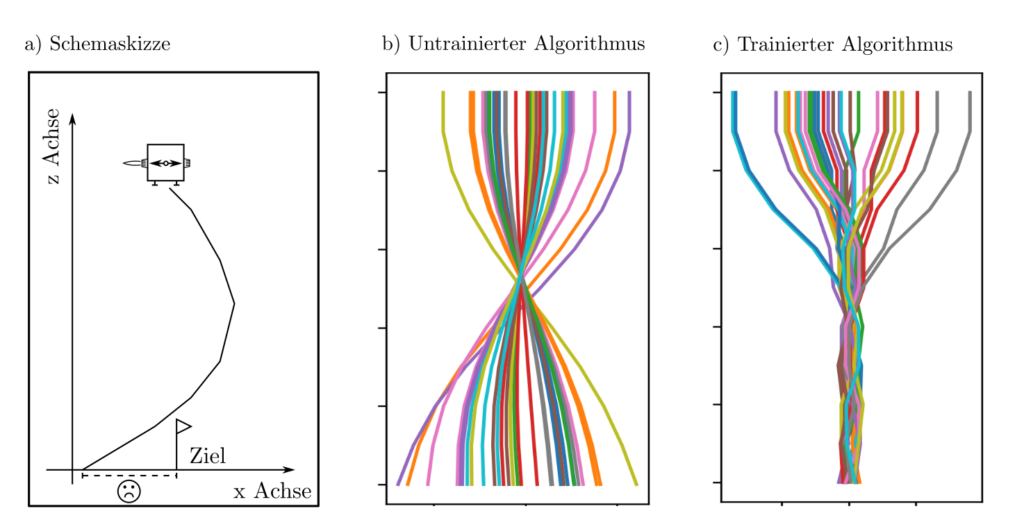
Beispiel: Adaptive Messdichteanpassung

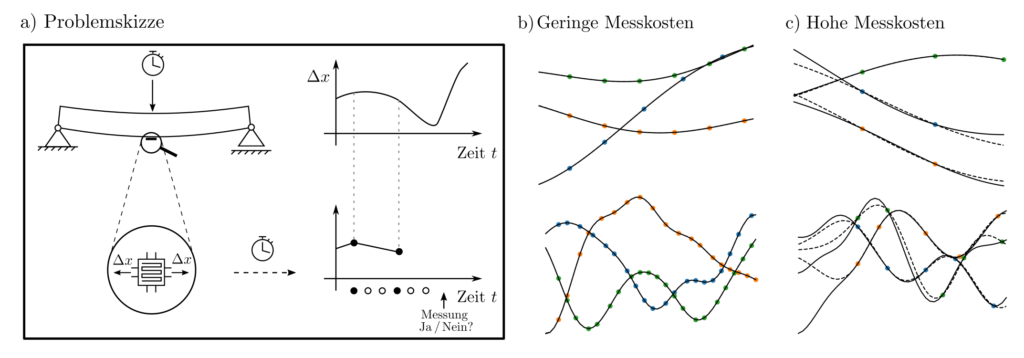
Ein Sensor soll das zeitliche Bewegungsverhalten eines Objektes so messen, dass es möglichst genau rekonstruierbar ist. Jede Messung kostet allerdings Geld; die Messzeitpunkte sind demnach ökonomisch zu wählen. Das Computermodell dieses Problemes beinhaltet zufällig generierte Funktionen, zu jedem Zeitpunkt die Option zu einer Bewegungsmessung, und am Ende des Versuchslaufes eine Aufwiegung von Meskosten und Rekonstruktionsfehler als Performancemass.

Beispiel: Adaptive Suchstrategie

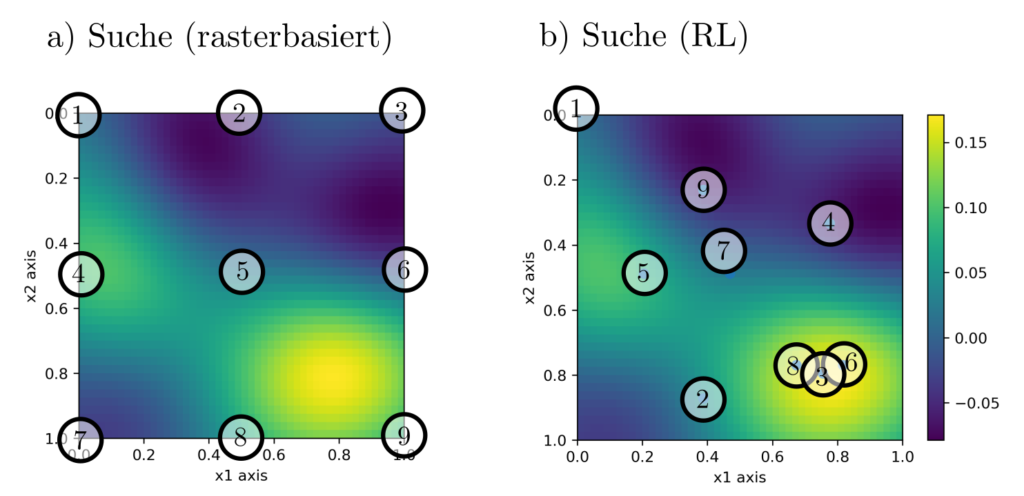
Auf einem mit Schadstoffen belasteten Grundstück sollen der Ort und die Schwere der Maximalbelastung festgestellt werden. Dazu können 9 Schadstoffmessungen an frei wählbaren Orten durchgeführt werden und der Algorithmus soll adaptiv auf Basis vorhergehender Messungen über den Ort der nächsten Messung entscheiden. Die Trainingsdaten bestehen aus Simulationen, die mutmasslich ähnliche Korrelationsstruktur aufweisen wie die Schadstoffverbreitung in der echten Welt.

Praktisches

Reinforcement learning kann für so gut wie alles verwendet werden, inklusive für Probleme hochdimensionaler Natur mit hohen Ansprüchen an die Lernfähigkeit des Algorithmus. Diese Flexibilität bedingt jedoch auch signifikante Nachteile. RL ist enorm datenhungrig, weist Stabilitätsprobleme auf und stellt hohe Modellierungsanforderungen an den Anwendenden. Dieser hat Zustands- und Aktionenräume so zu entwerfen, dass die Dynamik Markoveigenschaften hat und muss durch die Architektur der involvierten künstlichen neuronalen Netze Flexibilität und Regularität balancieren.

Ist ein Problem als etablierte konvexee Optimierungaufgabe formulierbar, sollte auf RL verzichtet werden. Für viele andere Probleme ist RL trotz seiner Tücken der einzige gangbare Ansatz. Da es sich um eine Methode handelt, an der weiterhin aktiv und intensiv geforscht wird, sind für die Zukunft eignifikante Fortschritte zu erwarten.

Code & Quellen

Beispielcode: OC_RL_class_def_2D_env-py , OC_RL_def_2D.py , OE_RL_control_trajectory.py , OC_RL_measurement_decisions.py , OC_RL_support_funs.py , OC_RL_trained_benchmark_def_2D.zip in unserem Tutorialfolder.

[1] Wiering, M., & Otterlo, M. v. (2012). Reinforcement Learning: State-of-the-Art. Berlin Heidelberg: Springer Science & Business Media.

[2] Fujimoto, S., van Hoof, H., & Meger, D. (2018). Addressing function approximation error in actor-critic methods. arXiv preprint arXiv:1802.09477, 2018.

[3] Raffin, A., Hill, A., Gleave, A., Kanervisto, A., Ernestus, M., & Dorman, N. (2021). Stable-Baselines3: Reliable Reinforcement Learning Implementations. Journal of Machine Learning Research. 22, (268), 1−8.