Optimal control: Robust optimal control
Problemstellung

Beim robusten optimal control soll ein System stabilisiert werden, dessen exakte dynamische Eigenschaften nicht bekannt sind und nur auf einen bestimmten Unsicherheitsbereich eingeschränkt werden können. Eventuell ist der Zustand des Systemes ausserdem nur unvollständig beobachtbar.
Trotzdem soll ein zeitabhängiger Input \(u(t)\) gefunden werden, der den Systemzustand \(x(t)\) stabilisiert, d.h. \(\lim_{t\rightarrow \infty} x(t)=0\) unabhängig von der eigentlichen Dynamik. Probleme dieser Art treten z.B. bei der Steuerung von Drohnen [1], Helikoptern, Festplattenauslesealgorithmen [2] und generell sobald die Steuerungsmechanismen eines Systems Unsicherheiten aufweisen.
Optimal control bei unbekannter Dynamik
Die Dynamik eines Systemes mit teilweise unbekannter Dynamik ist gegeben durch die Gleichung
$$ \dot{x}(t)=Ax(t)+Bu(t) ~~~~~~[A,B] \in Co([A_1,b_1], …, [A_n,B_n]), $$
welche Systemveränderungen \(\dot{x}\) mit den zeitabhängigen Zustandsgrössen \(x(t)\) und Steuerungsinputs \(u(t)\) koppelt. Die Matrizen \(A\) und \(B\) sollen dabei alle möglichen gewichteten Mittel \([\sum_{k=1}^n\lambda_k A_k, \sum_{k=1}^n \lambda_k B_k], \sum_{k=1}^n\lambda_k=1, \lambda_k \ge 0\) zwischen den Eckpunkten \([A_1, B_1], …, [A_n, B_n]\) annehmen dürfen; diese Menge wird auch konvexe Hülle \(Co\) genannt. Wären \(A\) und \(B\) bekannte konstante Matrizen, so würde es sich um ein klassisches Planungsproblem handeln.
Ein System \(\dot{x}=Ax\) ist stabil, wenn es eine quadratische Funktion \(V(x)=x^TPx, P\succeq 0\) gibt, sodass [3, p. 428] gilt
$$\dot{V}(x)=x^T(A^TP+PA)x <0.$$
Diese sogenannte Lyapunov Funktion beweist, dass es eine Energiefunktion gibt, die alle vom System generierbaren Trajektorien erklärt. Eine Feedbackmatrix \(K\) mit \(u(t)=Kx(t)\) ist gesucht, welche das System stabilisiert. Sie kann abgeleitet werden zu \(K=YQ\) aus dem Lösungen \(Q, Y\) des nachfolgenden semidefiniten Glechungssystemes für die Matrizen \(Q\) und \(Y\) [3, p. 428].
$$ Q=Q^T \succ 0, ~~~~~~~~~ (QA_i^T+A_iQ)+(Y^TB_i^T+B_iY) \prec 0~~~~i=1, …,n$$
Beispiel: Harmonischer Oszillator
Das folgende Beispiel illustriert Anwendung und Vorgehen. Ein schwingendes System wird in Massenproduktion hergestellt und in unterschiedlichen Situationen eingesetzt. Obwohl sich die Dynamik je nach Situation unterscheidet, soll eine einzige, universell gültige Feedbacksteuerung zur Schwingungsdämpfung verwendet werden.
Es sei \(s\) die Raumvariable und wie üblich denotieren Punkt und Doppelpunkt die erste bzw. zweite Zeitableitung. Eine harmonische Schwingung ist charakterisiert durch die Differentialgleichung
$$ \begin{align}\dot{s} & = — \omega s \\ x&=\begin{bmatrix} s \\ \dot{s} \end{bmatrix} \\ & \Rightarrow \dot{x}=\begin{bmatrix} \dot{s} \\ \ddot{s} \end{bmatrix} =\begin{bmatrix} \dot{s} \\ — \omega s \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -\omega & 0 \end{bmatrix} \begin{bmatrix} s\\ \dot{s} \end{bmatrix}= Ax. \end{align}$$
Dabei ist \(\omega >0 \) und die Resonanzfrequenz \(\sqrt{\omega}\) kann je nach Situation andere Werte annehmen. Es liege \(\omega\) zwischen \(1/2\) und \(3/2\) und der Steuerungsinput sei eine Beschleunigung; \(Bu=[0,0,u[^T\) mit \(B=[0,0,1]^T\). Es ist dann das folgende SDP zu lösen.
$$ \begin{align} \min_{Q,Y} ~~~& \operatorname{tr} (Q) \\ \text{s.t.} ~~~&Q \succ 0 ~~~~ \operatorname{tr} Q \ge 1 \\ &(Q A_1^T +A_1Q)+(Y^TB^T + BY) \prec 0 \\ &(Q A_2^T +A_2Q)+(Y^TB^T + BY) \prec 0 \\ & A_1 =\begin{bmatrix} 0 & 1 \\ ‑1/2 & 0 \end{bmatrix} ~~~~~~~A_2=\begin{bmatrix} 0 & 1 \\ ‑3/2 & 0\end{bmatrix} \end{align}$$
Dieses semidefinite Programm kann z.B. mit CVXPY [4] gelöst werden zu \(K\approx [-60,-9]^T\). Die Auswirkung dieser Feedbackmatrix ist in der untenstehenden Abbildung zu sehen.
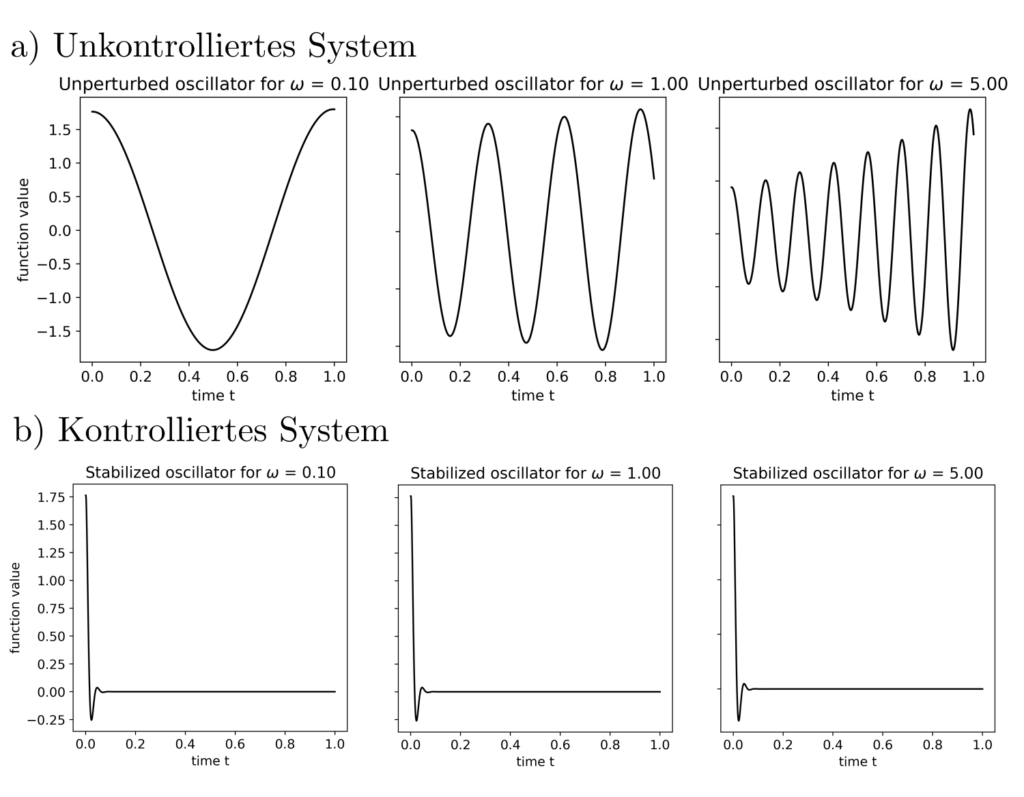
Es ist ersichtlich, dass die obige Steuerung die Systeme stabilisiert unabhängig von den genauen Eigenfrequenzen. Die triviale Steuerung \(u=-s\) z.B. tut dies nicht.
Unbekannter Zustand und zeitveränderliche Dynamik
Ist bei einem zu steuernden System der zeitabhängige Zustand \(x(t)\) nur durch ein Outputsignal \(y(t)=C_yx(t)\) erfassbar und die Dynamik
$$ \dot{x}=A(t)x(t)+Bu(t) ~~~~~~~A(t) \in Co([A_1, …, A_n]) $$
zeitveränderlich, so ist das System nur unter gewissen Umständen stabilisierbar. Die matrix \(A(t)\) ist eine zeitveränderliche lineare Kombination $$A(t)=\sum_{k=1}^n\theta_k(t)A_k ~~~~\sum_{k=1}^n \theta_k(t)=1, \theta_k(t)\ge 0.$$ Es ist ein Element der konvexen Hülle \(Co([A_1, …, A_n])\), das den Zusammenhang zwischen Systemveränderungen \(\dot{x}\) und Systemzustand \(x\) beschreibt. Der nur indirekt beobachtete Zustand \(x\) soll stabilisiert werden.
Solceh Probleme treten auf bei Systemen, die über eine grosse Bandbreite von Situationen hinweg stabil zu halten sind und deren Beschreibung nichtlineare Terme und unbeobachtete Konditionen enthält [5]. Diese Problemklasse beinhaltet die Entwicklung von Autopiloten für Luft- und Raumfahrtsysteme sowie die optimale Steuerung von chemischen Reaktionen in der Verfahrenstechnik [6].
SDP Formulierungen
Unter der Annahme, dass die Mischungskoeffiziente \(\theta_k(t)\) zu jeder Zeit bekannt seien, kann gezeigt werden, dass eine stabilisierbare höherdimensionale Einbettung von \(x\) existiert, wenn das semidefinite Gleichungssystem
$$\begin{align} &\begin{bmatrix} S & I \\ I & R \end{bmatrix} \succeq 0 \\ &N_R^T(A_kR + R A_k^T)N_R \prec 0 ~~~~ k=1, …, n \\ &N_S^T(A_kS + S A_k^T)N_S \prec 0 ~~~~ k=1, …, n \end{align}$$
eine Lösung \(S, R\) hat [3, pp. 428–431]. Hierbei sind \(N_R^T\) und \(N_S^T\) Matrizen, dessen Spalten die Basis der Nullräume von \(B^T\) respective \(C_y\) bilden. Mehr Details sind in [7, pp. 22–23] zu finden. Ist das Gleichungssystem lösbar, so kann das System
$$\begin{bmatrix} x \\ x_c \end{bmatrix} =\left( \underbrace{\begin{bmatrix} A(t) & 0 \\ I & 0\end{bmatrix}}_{\mathcal{G}} + \underbrace{\begin{bmatrix} 0 & B \\ I & 0 \end{bmatrix}}_{\mathcal{B}} \underbrace{\begin{bmatrix} A_c(t) & B_c(t) \\ C_c(t) & D_c(t) \end{bmatrix}}_{\Omega(t)} \underbrace{\begin{bmatrix} 0 & I \\C_y & 0 \end{bmatrix}}_{\mathcal{C}}\right) \begin{bmatrix}x \\ x_c \end{bmatrix}$$
nach der unbekannten closed loop state transition Matrix \(A_{cl}(t)=\mathcal{G}+\mathcal{B}\Omega(t) \mathcal{C}\) aufgelöst werden. Zudem kann die Bedingung $A_{cl}^T(t)P+PA_{cl}(t) \prec 0 ~~~~~ P \succ 0 $
erfüllt werden, sodass das System stabil ist, da es entlang aller möglichen Trajektorien Energie verliert. Wird für jedes \(k=1, …, n\) das Gleichungssystem
$$\begin{align} &(\mathcal{G}_k+\mathcal{B}\Omega_k\mathcal{C})^TP + P(\mathcal{G}_K + \mathcal{B}\Omega_k \mathcal{C}) \prec 0 \\ &P=\begin{bmatrix} S & (S‑R^{-1})^{1/2} \\ (S_R^{-1})^{1/2 T} & I \end{bmatrix} ~~~~~~\mathcal{G}_K=\begin{bmatrix} A_k & 0 \\ 0 & 0 \end{bmatrix}\end{align}$$
nach \(\Omega_k\) gelöst, so ergibt sich durch gewichtete Linearkombination der einzelnen Lösungen für \(\Omega_k\) eine zeitabhängige Gesamtlösung. Das System
$$ \begin{bmatrix} \dot{X} \\ \dot{X}_c \end{bmatrix} = \left( \begin{bmatrix} \sum_{k=1}^n \theta_k(t) A_k & 0 \\ 0 & 0 \end{bmatrix} + \begin{bmatrix} 0 & B \\ I & 0 \end{bmatrix} \left(\sum_{k=1}^n \theta_k(t) \Omega_k \right) \begin{bmatrix} 0 & I \\ C_y & 0 \end{bmatrix}\right) \begin{bmatrix}x \\ x_c \end{bmatrix}$$
ist stabil. Der vom Output \(y\) abgeleitete Steuerungsinput \(u\) ist demnach gegeben durch \(u(t)\) mit
$$\begin{align} u(t) &= \sum_{k=1}^n \theta_k(t) C_c^kx_c + \sum_{k=1}^n \theta_k(t) D_c^ky \\ \Omega_k&=\begin{bmatrix} A_c^k & B_c^k \\ C_c^k & D_c^k\end{bmatrix} \end{align}$$
wobei \(x_c\) sich entwickelt gemäss \(\dot{x}_c = \sum_{k=1}^n A_c^kx_c+\sum_{k=1}^n\theta_k(t) B_c^kC_yx\).
Beispiel: Schaltkreis
Ein Beispiel verdeutlicht das Vorgehen. Es sei ein Schaltkreis mit einem Widerstand, einer Spule, und einem Kondensator gegeben. Gemäss z.B. [8, pp. 10–11] ist der Zusammenhang zwischen Spannung \(V\) , Stromstärke \(I\), und Zeit \(t\) gegeben durch die vektorwertige Differentialgleichung
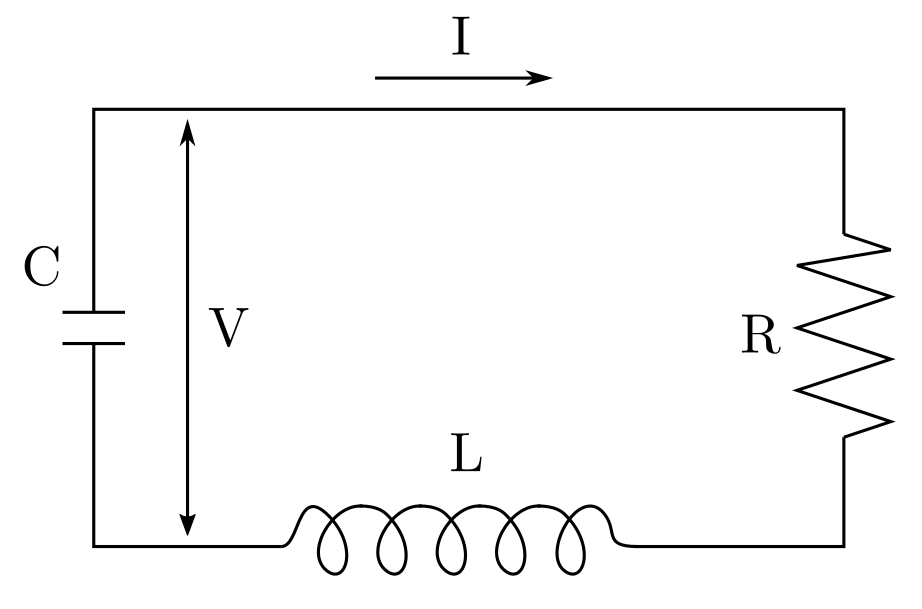
$$ \begin{bmatrix} \dot{V} \\ \dot{I}\end{bmatrix} = \begin{bmatrix}0 & — 1/C \\ 1/L & ‑R/L\end{bmatrix} \begin{bmatrix} V\\ I \end{bmatrix} + \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} $$
wobei \(R\) der Widerstand, \(L\) die Induktivität der Spule, und \(C\) die Kapazität des Kondensators ist. Wir gehen davon aus, dass
- die Änderung von Spannung und Stromstärke über den Regelungsinput \([u_1,u_2]^T\) gesteuert werden kann
- \(C\) und \(L\) zwischen 1 und 10 variieren
- nur die Stromstärke beobachtbar ist und die Spannung nicht gemessen wird.
Trotz der problematischen Konditionen 2. (veränderliche Schaltkreisparameter) und 3. (Spannung nicht beobachtbar) soll das System stabilisiert werden. Wir wenden die obig präsentierten Gleichungen an udn erhalten die folgende Kette von semidefiniten Gleichungssystemen, die wir z.B. mit CVXPY lösen können.
$$\begin{align}1.~~~~ \text{find} & ~~~R, S \\ s.t. &~~~ \begin{bmatrix} R & I \\ I &S \end{bmatrix} \succeq 0 \\ &~~~ \begin{bmatrix} 1 & 0\end{bmatrix} (S A_k + A_k^TS) \begin{bmatrix} 1 \\ 0 \end{bmatrix} <0 ~~~~~~k=1, …, 4 \\ &~~~ A_1=\begin{bmatrix} 0 & ‑1 \\ 1 & ‑R\end{bmatrix} ~~~~~A_2=\begin{bmatrix} 0 & ‑0.1 \\ 1 & ‑R\end{bmatrix} \\ & ~~~A_3=\begin{bmatrix} 0 & ‑1 \\ 0.1 & ‑0.1R\end{bmatrix}~~~~~A_4=\begin{bmatrix} 0 & ‑0.1 \\ 0.1 & ‑0.1R\end{bmatrix}\\2.~~~~ \text{find} & ~~~\Omega_k \\ s.t. &~~~(\mathcal{G}_k + \mathcal{B}\Omega_k \mathcal{C})^TP+P(\mathcal{G}_k+\mathcal{B}\Omega_k\mathcal{C}) \prec0 \\ & ~~~\mathcal{G}_k= \begin{bmatrix} A_k & 0 \\ 0 & 0\end{bmatrix} ~~~~~\mathcal{B}=\begin{bmatrix} 0& 0& 1&0\\0&0&0&1\\1&0&0&0\\0&1&0&0\end{bmatrix} ~~~~~\mathcal{C}=\begin{bmatrix} 0&0&1&0\\ 0&0&0&1\\ 0&1&0&0\end{bmatrix} \end{align}$$
Das Resultat ist in der untenstehenden Abbildung sichtbar.
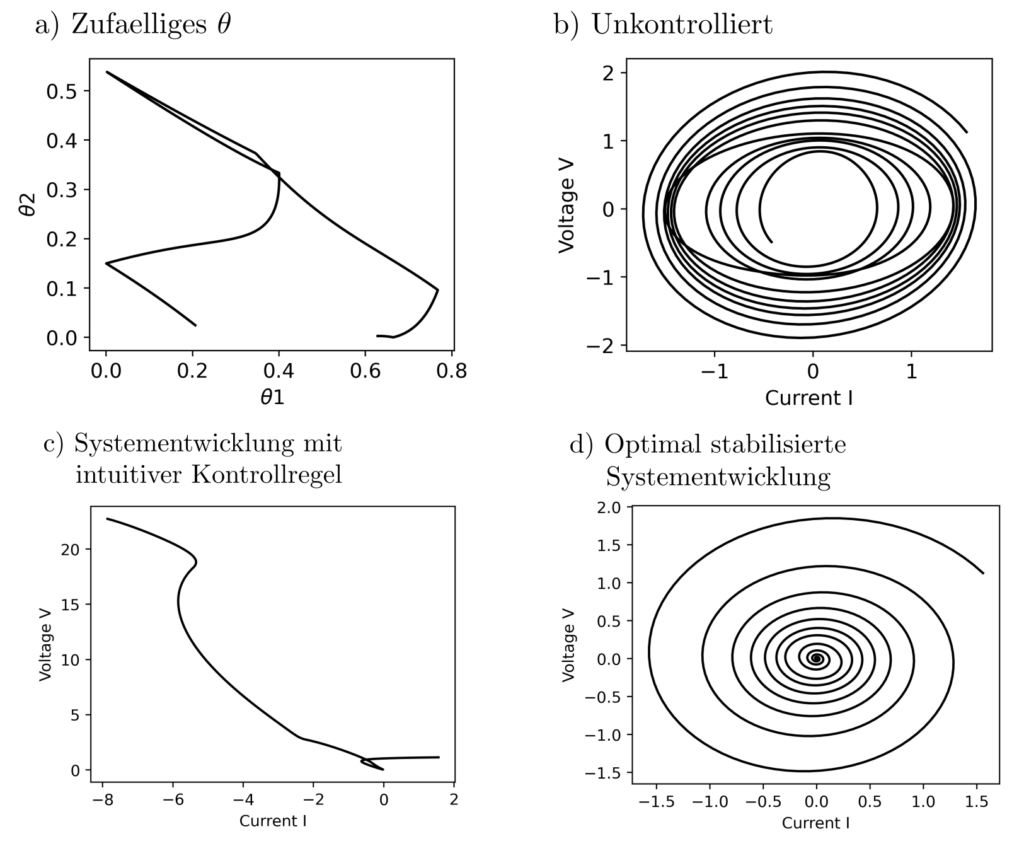
In der Tat ist das System stabil. Dies ist nicht der Fall, wird der Kontrollinput nach intuitiven, manuell erdachten Regeln gewählt oder sich selbst überlassen. Der Ansatz für das optimal control von nur partiell beobachteten Systemen mit teilweise unbekannter Dynamik liefert also einen echten Mehrwert.
Code & Quellen
Beispielcode: OC_harmonic_oscillator_3.py , OC_harmonic_oscillator_4.py in unserem Tutorialfolder.
[1] AlSwailem, S.I. (2004). Application of Robust Control in Unmanned Vehicle Flight Control System Design. Dissertation Cranfield University, Cranfield.
[2] Postlethwaite, I., Turner, M. C., Guido, H. (2007). Robust Control Applications. Annual Reviews in Control, 31, (1), 27–39
[3] Wolkowicz, H., Saigal, R., & Vandenberghe, L. (2012). Handbook of Semidefinite Programming: Theory, Algorithms, and Applications. Berlin Heidelberg: Springer Science & Business Media.
[4] Diamond S., & Boyd S., (2016). CVXPY: A Python-embedded modeling language for convex optimization. Journal of Machine Learning Research, 17(83), 1–5.
[5] Leith, D. J., & Leithead, W. E. (1998). Appropriate realisation of MIMO gain-scheduled controllers. International Journal of Control, 70, (1), 13–50.
[6] Klatt, K. U., & Engel S. (1998). Gain-scheduling trajectory control of a continuous stirred tank reactor. Computers & Chemical Engineering, 22, 491–502.
[7] Boyd, S., El Ghaoui, L., Feron, E., & Balakrishnan, V. (1994). Linear Matrix Inequalities in Systems and Control Theory. Philadelphia: SIAM Studies in Applied and Numerical Mathematics.
[8] Scheinerman, E. R. (2013). Invitation to Dynamical Systems. New York: Courier Corporation.
