Stochastisches optimal control - Atlas optimization

Optimal control: Stochastisches optimal control

Definition

Ein System enthält in gewissem Rahmen frei zu wählende Steuerungsinputs und soll durch diese stabilisiert werden. Die Dynamik des Systems, d.h. der Einfluss von Steuerungsinput und momentanem Zustand auf den zukünftigen Zustand seien bekannt aber der Systemverlauf sei weiterhin von zufälligen Störgrössen beeinflusst..

Dies ist eine Erweiterung des optimal controls bei bekannter Dynamik und bekanntem Zustand um zufällige Störgrössen. Das linear-quadratische Gaussche Reglerproblem (LQG) ist ein Beispielproblem dieser Problemklasse, bei der die Störgrössen normalverteilt sind.

LQG control

Das dynamische Modell beim LQG kann geschrieben werden als

$$ x_{k+1}=Ax_k+Bu_k+w_k$$

mit $x_k, x_{k+1}$ typischerweise vektorwertigen Zuständen zu Zeitpunkten $t=k, k+1$, $u_k$ den Steuerungsinputs, $w_k$ den zufälligen Störgrössen und $A, B$ Matrizen. Die Steuerungsinputs seien so zu wählen, dass eine Stabilisierung des Systemes erreicht wird.

Seien die die Systemdynamik beschreibenden Matrizen $A, B$ bekannt, die Schwankungsbreite von $w$ quantifizierbar durch die Kovarianzmatrix $W$ und der Steuerungsinput $u_k, k=1, … T $ sei so zu wählen, dass die durchschnittliche Energie minimiert wird. Formal ergibt sich das Optimierungsproblem

$$\min_{x_1, …, x_T, u_1, …, u_T} \lim_{T\rightarrow \infty} \frac{1}{T} E\left[ \sum_{k=0}^T \|x_k\|^2_Q + \|u_k\|^2_R\right] $$

wobei $\|x_k\|^2_Q=x_k^TQx_k$ und $ \|u_k\|^2_R=u_k^TRu_k$ Masse sind für die Kosten von Zustand $x_k$ und Steuerungsinput $u_k$ und $E[\cdot]$ ist der Erwartungswert.

SDP Formulierung

Der optimale Steuerungsinput $u_k$ ergibt sich nach der Gleichung [1] $u_k=Z_{xu}^T(Z_{xx})^{-1} x_k$ wobei $Z_{xx}$ und $Z_{xu}$ die Lösungen für das nachfolgende semidefinite Programm sind [2].

$$\begin{align} \min_{Z_{xx}, Z_{xu}, Z_{uu}} ~~~&\operatorname{tr} (QZ_{xx}) + \operatorname{tr} (R Z_{uu}) \\ s.t. ~~~& \begin{bmatrix} Z_{xx} & Z_{xu} \\ Z_{xu}^T & Z_{uu} \end{bmatrix} \succeq 0 \\ & Z_{xx}-AZ_{xx}A^T‑AZ_{xu}B^T — BZ_{xu}^TA^T — B Z_{uu}B^T=W\end{align}$$

Die zu minimierende Funktion $\operatorname{tr} (QZ_{xx}) + \operatorname{tr} (R Z_{uu})$ quantifiziert erwartete Kosten (Geld, Zeit, Energie, Fehler) über den Zusammenhang $$E[X^TQx+u^TRu]=\operatorname{tr}(Q E[xx^T])+\operatorname{tr}(RE[uu^T])=\operatorname{tr}(QZ_{xx})+\operatorname{tr}(RZ_{uu}).$$ $Z_{xx}$ und $Z_{uu}$ sind demnach interpretierbar als Kovarianzmatrizen der zufällig verteilten Grössen $x$ und $u$ und die Gleichung $u_k=Z_{xu}^T(Z_{xx})^{-1}x_k$ ist gerade der bedingte Erwartungswert von $u_k$ gegeben $x_k$ und die durch $Z_{xxx}, Z_{xu}, Z_{uu}$ determinierte energieminimierende Wahrscheinlichkeitsverteilung.

Beispiel: Pendelsteuerung

Im folgenden ausführlichen Beispiel wird das Ziel verfolgt, ein von zufälligen Effekten beeinflusstes Pendel zu stabilisieren. Wir gehen davon aus, ein Pendel startet in zufälliger (aber kleiner) Auslenkung $\varphi$ aus der Gleichgewichtslage.

Die Pendelbewegung folgt dann normalen physikalischen Gesetzmässigkeiten mit der Ausnahme, dass zusätzlich noch zufällige und von uns weder vorhersehbare noch kontrollierbare Effekte eine Kraft und somit auch eine Beschleunigung auf das Pendel bewirken.

Abbildung 1: Illustration der Pendeldynamik durch Angabe der zeitlichen Entwicklung des Auslenkungswinkels $\varphi$ und seiner zeitlichen Ableitunge $\dot{\varphi}$ und $\ddot{\varphi}$. Die ersten beiden Grafiken (a) zeigen die Systemevolution in Abwesenheit von Zufallseffekten, die letzten Grafiken (b) zeigen die Systemevolution in Anwesenheit von Zufallseffekten auf $\ddot{\varphi}$.

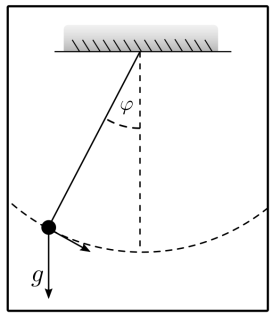
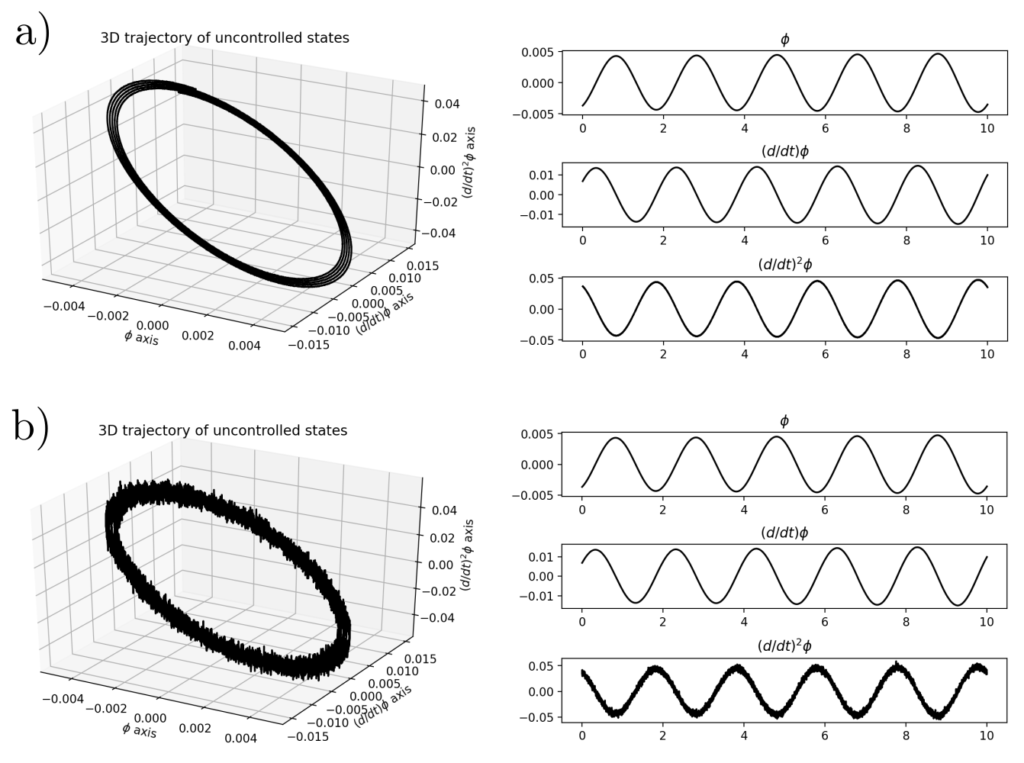
Man beachte, dass die Grafik das für ein Pendelschwingen erwartete Verhalten zeigt. Ist die Auslenkung $\varphi$ maximal, dann ist die Geschwindigkeit $\dot{\varphi}=0$ und die Beschleunigung $\ddot{\varphi}$ minimal. Ist die Auslenkung $\varphi=0$, so ist die Geschwindigkeit $\dot{\varphi}$ maximal und die Beschleunigung $\ddot{\varphi}$ wechselt von positiv zu negativ bzw. umgekehrt.

Pendelgleichungen

Die von der Gewichtskraft $g$ induzierte Beschleunigung in Schwingrichtung ist $-g\sin(\varphi)$. Weiterhin wirken die zufälligen Effekte $w$ und wir nehmen an, der von uns wählbare Steuerungsinput $u$ beeinflusst direkt die beschleunigung, sodass gilt

$$\ddot{\varphi}_k = ‑g \sin(\varphi_k) + w_k + u_k ~~~~~~~k=0, …, T .$$

Die Zustandsgleichung koppelnd verschiedene Grössen über sukzessive Zeitschritte hinweg kann geschrieben werden als

$$ \underbrace{\begin{bmatrix} \varphi_{k+1} \\ \dot{\varphi}_{k+1} \\ \ddot{\varphi}_{k+1} \\ \sin(\varphi_{k+1}) \\ \cos(\varphi_{k+1}) \end{bmatrix}}_{x_{k+1}} = \underbrace{\begin{bmatrix} 1 & \Delta t & 0 & 0& 0 \\ 0 & 1 & \Delta t & 0 & 0 \\ 0& 0& 0& ‑g & 0 \\ 0 & \Delta t & 0 & 1 & 0 \\ 0&0&0&0&0\end{bmatrix}}_{A}\underbrace{\begin{bmatrix} \varphi_{k} \\ \dot{\varphi}_{k} \\
\ddot{\varphi}_{k} \\ \sin(\varphi_{k}) \\ \cos(\varphi_{k})
\end{bmatrix}}_{x_{k}} + \underbrace{\begin{bmatrix} 0 \\ 0\\ 1 \\ 0\\0 \end{bmatrix}}_{B} \underbrace{\begin{bmatrix} u_k\end{bmatrix}}_{u_k} + \underbrace{\begin{bmatrix} 0\\0\\w_k\\0\\0 \end{bmatrix}}_{w_k}.$$

Dabei werden die für kleine Winkel gültigen Approximationen

$$\begin{align} \sin (\varphi+\Delta \varphi)&\approx \sin\varphi+\Delta \varphi \cos \varphi\approx \sin \varphi + \Delta t \dot{\varphi} \cos \varphi \approx \sin \varphi + \Delta t \dot{\varphi} \\ \cos(\varphi+\Delta\varphi) &\approx \cos \varphi — \Delta \varphi \sin \varphi \approx \cos \varphi — \Delta t \dot{\varphi} \sin \varphi \approx \cos \varphi \end{align}$$

benutzt, um die letzten zwei Reihen der Gleichung zu erstellen.

Optimierungslösung

Möchten wir nun eine matrix $K$ finden, sodass der Steuerungsinput $u_k=Kx_k$ das System stabilisiert, so ist das Optimierungsproblem

$$\begin{align} \min_{Z_{xx}, Z_{xu}, Z_{uu}} ~~~& \sum_{i=1}^3 (Z_{xx})_{ii} +(Z_{uu})_{ii} \\ s.t. ~~~& \begin{bmatrix} Z_{xx} & Z_{xu} \\ Z_{xu}^T & Z_{uu} \end{bmatrix} \succeq 0 \\ & Z_{xx}-AZ_{xx}A^T‑AZ_{xu}B^T — BZ_{xu}^TA^T — B Z_{uu}B^T=W\end{align}$$

zu lösen. Dabei sind $A$ und $B$ wie im vorigen Abschnitt beschrieben, $w$ ist eine $5 \times 5$ Matrix von $0$ en mit Ausnahme des Eintrages $W_{33}=\sigma_w^2$ der Varianz des Zufallseffektes auf die Beschleunigung und das resultierende Steuersignal ist $u_k= Kx_k=Z_{xu}^T(Z_{xx})^{-1}x_k$.

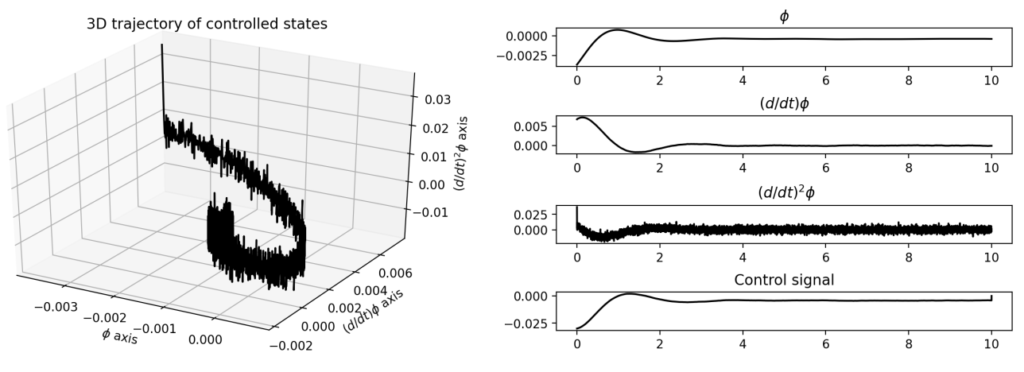
Praktisches

Soll das obige Lösungsvorgehen auf andere Systeme übertragen werden, sind einige Hinweise zu beachten. Die Systemdynamik muss linear sein und somit formulierbar als $$x_{k+1}=Ax_k+Bu_k+w_k$$ wobei die $w_k$ unabhängige Zufallsvariablen mit bekannter Kovarianzmatrix sein müssen. Sind die $w_k$ untereinander korrelliert, muss die gesamte Optimierungsgleichung in einen höherdimensionalen Raum eingebettet werden, in den die $x_1, …, x_k$ und $w_1, …, w_k$ gleichzeitig einbezogen werden.

Schon beim Pendelbeispiel war der Zustand $x_k$ 5‑dimensional mit zwei Hilfsdimensionen, die $\sin \varphi_k$ und $\cos \varphi_k$ dokumentiert haben. Die Definition des Zustandsvektors muss vom Anwendenden selber durhgeführt werden und kann durchaus kompliziert werden. Oft sind Tricks und Approximationen nötig, um nichtlineare Gleichungen in eine sinnvoll verwendbare linearisierte Form zu überführen.

Code & Quellen

Beispielcode: OC_stochastic_control_1.py , OC_stochastic_control_2.py in unserem Tutorialfolder.

[1] Balakrishnan, V., & Vandenberghe, L. (2003). Semidefinite programming duality and linear time-invariant systems. IEEE Transactions on Automatic Control, 48,(1), 30–41.

[2] Kamgarpour, M., Summers, T. (2017). On infinite dimensional linear programming approach to stochastic control. 20th IFAC World Congress (IFAC 2017), Toulouse, France, July 9–14. IFAC-PapersOnLine, 50, (1), 6148 — 6153.