Optimal design: Übersicht
Definition
Eine Aufgabe fällt in den Bereich des optimal design, wenn sie die optimale Wahl von Produktparametern beinhaltet. In Abgrenzung zu optimal control und optimal estimation wird dabei weniger Wert gelegt auf zeitveränderliche Systeme und das Schätzen unbekannter Zusammenhänge.
Stattdessen sind die Fragestellungen weniger datengetrieben und mehr abgeschlossener, prä-analytischer Natur: Gegeben konkrete Informationen betreffen das Ziel des Designvorhabens, welche Wahl von Parametern maximiert den Erfolg des mit solchen Parametern ausgestatteten Produktes?
Einsatzbereich
Dabei kann es sich bei einem solchen Produkt sowohl um ein physisches Objekt handeln als auch um zeitminimierende Ablaufpläne oder um maximaleffiziente Experimentkonfigurationen, Transportrouten, Ressourcenallokationen, oder Netzwerkdesigns. Diese Liste gibt einen grob unvollständigen Überblick.
Die Anwendungen sind enorm vielfältig und verfügen oft über eine direkte betriebswirtschaftliche Komponente. Dies ist entwicklungsgeschichtlichen Hintergründen geschuldet und der Tatsache, dass Zeitaufwand und Kosten sich unmittelbar aufdrängende und einfach zu interpretierende Erfolgsmasse sind, deren Minimierung von allgemeinem Interesse ist. In seiner allgemeinsten Form
$$ \begin{align} \min_{x\in D} ~~~& f(x) \end{align}$$
jedoch inkludiert das optimal design die Optimierung von z.B. Unsicherheiten, Stabilitäts- und Flexibilitätsmassen, physikalischen aber auch psychologischen Kennzahlen und beliebigen sonstigen Produktwirkungen. Je allgemeiner jedoch die Funktion, umso weniger Zusatzstruktur kann genutzt werden, um den Lösungsprozess zu vereinfachen.
Beispiel
Ein Volumen \(V\) soll in einer Box verpackt werden. Je nach Dimensionierung der Seitenlängen der Box wird dazu verschieden viel Verpackungsmaterial benötigt. Das Optimierungsproblem lautet dann
$$ \begin{align} \min_{x_1, x_2, x_3} ~~~& F(x_1,x_2,x_3) \\ \text{s.t.} ~~~&x_1x_2x_3=V \end{align}$$
wobei \(F(x_1,x_2,x_3)=2[x_1x_2+x_2x_3+x_3x_1]\) die Fläche der Box ist und somit den Verpackungsmaterialverbrauch quantifiziert. Dieses Problem lässt sich leicht von Hand lösen.
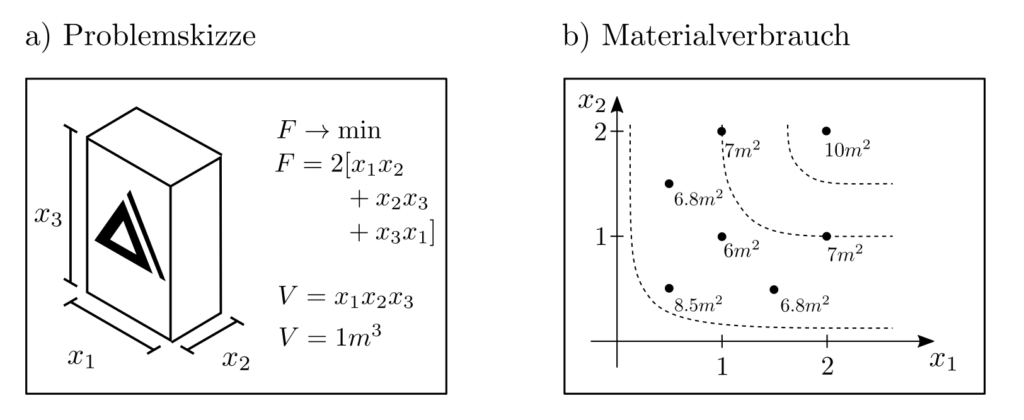
Werden die unsinnigen Grenzfälle \(x_k=0, k=1, 2, 3\) und \(V=0\) ausgeschlossen, dann kann die Nebenbedingung umgewandelt werden zu der Gleichung \(x_3=(x_1x_2)^{-1}V\). Das Minimum wird erreicht, wenn \(\nabla F =0 \), also
$$\begin{bmatrix} \frac{\partial}{ \partial x_1} F \\ \frac{\partial}{\partial x_2} F \end{bmatrix} = \begin{bmatrix} 2 x_2 — \frac{V}{x_1^2} \\ 2x_1- \frac{V}{x_2^2} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
Das ist genau dann der Fall, wenn \(x_1^2x_2=x_2^2x_1=V\) und somit \(x_1=x_2=(x_1x_2)^{-1}V=x_3\). Das impliziert direkt \(x_1=x_2=x_3 =V^{1/3}\), sodass die optimale Lösung in der Wahl einer kubischen Verpackung liegt. In der Realität müssen natürlich noch weitere Bedingungen berücksichtigt werden: Transport‑, Lager, und Fabrikationsfähigkeit der Verpackung hinauslaufend auf Grössenbeschränkungen sowie die Kosten des gesamten Fabrikationsprozesses und nicht nur des Verpackugnsmateriales. Es entsteht dann ein geometrisches programm, dessen Lösung nicht mehr offensichtlich ist.
Problemklassen
Überraschend viele praxisrelevante Aufgabenstellungen lassen sich als statisches Designproblem formulieren. Dies beinhaltet auch einige mit expliziter Zeitabhängigkeit. Wir beschränken uns im folgenden auf Probleme, für die zuverlässige Lösungsalgorithmen verfügbar sind. Diese nicht abschliessende Problemklassenübersicht schliesst einige interessante nichtllineare Probleme aus, die zwar nicht ins Schema passen, sich aber trotzdem mit globalen Optimierungsheuristiken und einem an handarbeit lösen lassen.
Experimentendesign
Beim Experimentendesign geht es darum, Einzelexperimente zu einer maximal wirksamen Kombination anzuordnen. Dabei mag das Ziel die Detektierbarkeit einer bestimmten Kenngrösse sein oder die Minimierung der Unsicherheiten der Aussagen, die aus der Experimentenkombination abgeleitet werden können.
Nebenbedingungen beschränken die für die Experimente zur Verfügung stehenden Ressourcen oder die Gleichzeitigkeit der Versuchsdurchführung. Die Produkte dieser Optimierung sind unsicherheitsminimierende Experimentenkombinationen.
Ablaufplanung
Ein Ablaufplan wird dazu verwendet, die Reihenfolge und Bearbeitungs-verantwortlichkeit von Aufgaben festzulegen. Ein typisches Beispiel ist die Maschinenbelegungsplanung: Diverse Rohstoffe müssen von Maschinen in Produkte umgewandelt werden.
Dabei erledigen verschiedene Maschinen verschiedene Arbeitsschritte in unterschiedlicher Geschwindigkeit und es ist eine Arbeitsabfolge so zu finden, dass sämtliche Deadlines eingehalten werden und die Gesamtbearbeitungsdauer minimiert wird. Die mathematisch optimale Ablaufplanung ist der grosse Bruder der ad-hoc Planung mit Gantt Diagrammen. Die Produkte dieser Optimierungen sind zeitminimierende Ablaufpläne.
Transport und Ressourcenallokation
Das travelling salesperson Problem ist eines der ältesten und offensichtlichsten Logistikprobleme. Eine vorgegebene Menge von Orten soll besucht werden in einer Sequenz, die die Gesamtdauer der Reise minimiert. Das Problem ist bewiesenermassen eines der schwierigsten mathematischen Probleme.
Trotzdem existieren Algorithmen, die zuverlässig selbst noch kompliziertere Transportprobleme mit diversen Orten, Gütern, Lieferkapazitäten, und Randbedingungen lösen können. Die Produkte dieser Optimierungen sind kostenminimierende Transportrouten.
Topologie- und Netzwerkdesign
Netzwerde und deren topologische Eigenschaften spielen eine grosse Rolle in der mathematischen Modellierung von Nachbarschaftszusammenhängen. Sie sind wichtig für die Darstellung von Sachverhalten betreffend etwa den Fluss von Gütern, Kräften, oder logischen Zusammenhängen.
Da Netzwerke häufig den formalen Rahmen für die in einem Optimierungsproblem auftretenden Randbedingungen stellen, garantiert deren optimales Design sinnvolles Verhalten der in diesem netzwerk fliessenden Entitäten.
Praktisches
Je nach genauer Problemformulierung und Nebenbedingungen ist eine Lösung der obigen Optimierungsprobleme einfach bis umöglich. Manche Transport- und Ablaufpläne lassen sich als lineares Programm schreiben und sind demnach unproblematisch, während Experimentendesign in der Regel auf semidefinite Programmierung hinausläuft und damit numerisch anspruchsvoller doch noch immer zuverlässig lösbar ist.
Sobald jedoch logische Beschränkungen und diskrete Objekte auftreten, muss gemischt-ganzzahlige Optimierung betrieben werden. Dann können keinerlei Konvergenzgarantien ausgesprochen werden . Leider ist dies häufig der Fall, sobald nichttriviale Nebenbedingungen berücksichtigt werden müssen. Die grosse Menge logistischer Literatur ist dennoch ein Zeichen für die praktischen Erfolge und die Wirksamkeit der Herangehensweise.
Code
Beispielcode: OD_product_packaging.py in unserem Tutorialfolder
