Optimal design: Ablaufplanung
Definition
Beim Design von Ablaufplänen (= Scheduling) wird das Ziel verfolgt, eine Menge von unterinander abhängigen Verwendungen so zu timen, dass der zur Durchführung aller Aufgaben aufzubringende Gesamtaufwand minimiert wird.
Bei den Verwendungen kann es sich um industrielle Produktionsprozesse, Personaleinsätze, oder simple Raumbelegungen handeln. Illustrationen und Qualitätskriterien für Ablaufpläne sind schon seit dem frühen 20.ten Jahrhundert bekannt und die zu dieser Zeit entstandenen Gantt ‑Diagramme werden noch immer verwendet. Mit ihnen können bereits existierende Ablaufpläne in Form von Balkendiagrammen visualisiert werden, sodass die Kommunikation der Planinhalte und ein eventuelles Troubleshooting vereinfacht werden.
Der Entwurf von Ablaufplänen geschieht entweder manuell nach heuristischen Regeln oder via optimierungsalgorithmus. Das nachfolgende Beispiel illustriert beide Vorgehen.
Beispiel: Problemstellung
Eine Maschine habe 4 Jobs \(J_1, …, J_4\) auszuführen. Diese Jobs verbrauchen Ressourcenmengen \(r_1, …, r_4\) und benötigen Prozessierungszeiten \(p_1, …, p_4\)
| \(p_1\) | \(p_2\) | \(p_3\) | \(p_4\) | in Tagen | \(r_1\) | \(r_2\) | \(r_3\) | \(r_4\) | in Tonnen | |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 6 | 10 | 12 | 1 | 1 | 1 | 1 |
Die Kosten für die Lagerung der Ressourcen sei direkt proportional zu gelagerter Ressourcenmenge und Lagerzeit und soll minimiert werden. Das Problem ist klein und einfach zu analysieren und lösen. Dazu werden alle potentiell möglichen Gantt-Diagramme geplottet.
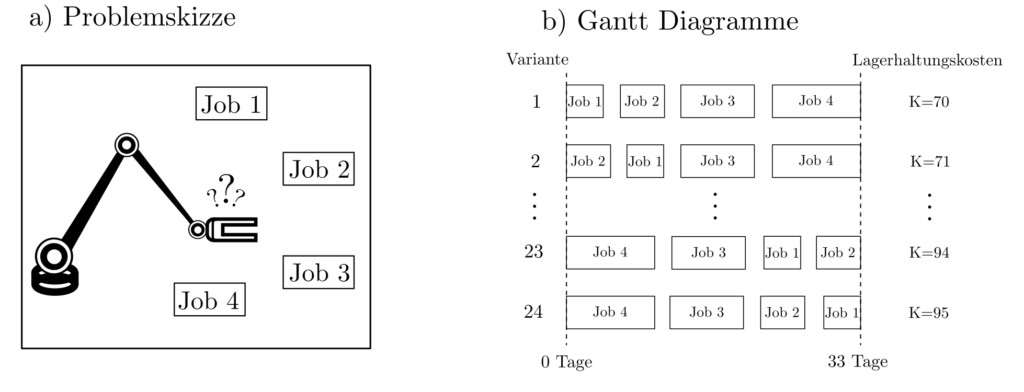
Beispiel: Kostenoptimierung
Die Kosten \(K\) errechnen sich als Summe von zu lagernden Ressourcen und Lagerdauern nach der Gleichung
$$\begin{align} K & = r_1(\text{Lagerungsdauer Ressourcen Job1})+ r_2(\text{Lagerungsdauer Ressourcen Job2})+… \\ & =\sum_{j=1}^4 r_jC_j \end{align}$$
wobei \(C_j\) der Komplettierungszeitpunkt von Job \(j\) ist. Nach Vergleich aller Varianten ergibt sich der beste Ablaufplan als
$$\text{Job}_1 \rightarrow \text{Job}_2 \rightarrow \text{Job}_3 \rightarrow \text{Job}_4 \text{ mit } K=r_1 5+r_2 11+ r_3 21+r_4 33=70. $$
Es lässt sich sogar im Allgemeinen zeigen [1, p. 131], dass für das obige System eine Anordnung nach aufsteigenden prozessierungsdauern optimal ist. Sind die Ressourcenmengen \(r_1, …, r_n\) nicht alle gleich, so gilt die WSPT rule (weighted shortest processing time first): die aufsteigende Anordnung gemäss der Quotienten \(r_jp_j^{-1}\) ist der optimale Ablauf und löst das Optimierungsproblem
$$\min_{\text{Ablaufplan}} \sum_{j=1}^n r_jC_j.$$
Verallgemeinerungen
Sind mehrere unterschiedliche Ressourcen, verarbeitende Maschinen, und Nebenbedingungen vorhanden oder soll ein anderes Qualitätskriterium optimiert werden, dann existieren mit hoher Wahrscheinlichkeit keine nach einfachen Regeln manuell konstruierbaren optimalen Ablaufpläne mehr.
Stattdessen muss auf Optimierungsalgorithmen zurückgegriffen werden. Oft handelt es sich um gemischt-ganzzahlige Optimierungsprobleme, die aus rechentechnischer Sicht schwierig zu lösen sind. Ein Lagerhaltungskosten minimierender Ablaufplan für \(n\) Jobs auf \(m\) Maschinen kann formuliert werden als das Optimierungsproblem [1, p. 134]
$$\begin{align} \min ~~~& \sum_{i=1}^m \sum_{j=1}^n \sum_{k=1}^nR_{ijk} p_{ij} x_{ikj} && \\ \text{s.t.} ~~~& \sum_{i=1}^m \sum_{k=1}^n x_{ikj}=1 &&j=1, …, n \\ & \sum_{j=1}^m x_{ikj} \le 1 && i=1, …,m ~ k=1, …, n \\ & x_{ikj}\in \{0,1\} && i=1, …, m ~ k=1, …, n ~ j=1, …, n \end{align}$$
Dabei ist \(p_{ij}\) die Prozessdauer von Job \(j\) auf Maschine \(i\) und \(x_{ikj}\) eine binäre Indikatorvariable anzeigend ob Job \(j\) auf Maschine \(i\) an \(k\)-letzter Stelle ausgeführt wird. Die Nebenbedingungen garantieren, dass jeder Job genau einmal vergeben wird. Der Term \(R_{ijk}\) repräsentiert die Ressourcenmengen, die zum \(k\)-letzten Zeitpunkt für die Verarbeitung auf Maschine \(i\) gelagert werden. Es sind dies die Ressourcenmengen späterer Projekte auf Maschine \(i\) , welche über die Zeitdauer \(p_{ij}\) gelagert werden müssen. Daher gilt:
$$R_{ijk} = \begin{cases} kr ~~~~~~~~~~~\text{ falls } r_1=r_2= … = r_n =:r \\ \sum_{l\le k} x_{ikj}r_j \text{ sonst }\end{cases} $$
Für den Fall ungleichen Ressourcenverbrauches ist das Optimierungsproblem nichtlinear in den Indikatorvariablen \(x_{ikj}\) und kann nur approximativ gelöst werden z.B. über Relaxationen basierend auf semidefiniter Programmierung [2].
Beispiel: m Maschinen, n Jobs
verwenden jedoch alle Jobs die gleichen Ressourcenmengen, dann ist mit \(R_{ijk}=kr\) als momentane Lagermenge auf Maschine \(i\) das Optimierungsproblem formulierbar als lineare programm mit der Zielfunktion
$$ \sum_{i=1}^m\sum_{j=1}^n \sum_{k=1}^nrkp_{ij}x_{ikj}$$
und denselben Nebenbedingungen wie oben. Dieses Problem kann gelöst werden z.B. mit dem Solver GLPK [3] für gemischt-ganzzahlige lineare Programmierung. Wie das nachfolgende Beispiel zeigt, sind die optimalen Resultate nicht durch intuitives raten einer Jobabfolge oder Tabellierung aller potentiellen Lösungen zu erreichen. Es sollen Ressourcenlagerkosten für 12 Jobs auf 3 Maschinen minimiert werden. Die Prozessdauern \(p_{ij}\) sind wie folgt
| Maschine\ Job | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1/2 | 2 | 1 | 1/2 | 1/4 | 3 | 2 | 1/8 | 1 | 2 | 1 |
| 2 | 1/2 | 2 | 1 | 1/2 | 1/4 | 3 | 2 | 1/8 | 1 | 2 | 1 | 1 |
| 3 | 2 | 1 | 1/2 | 1/4 | 3 | 2 | 1/8 | 1 | 2 | 1 | 1 | 1/2 |
Das entsprechende lineare Programm ist
$$\begin{align} \min ~~~ & q^T \operatorname{vec} (x) \\ \text{s.t.} ~~~ & x^TA=\vec{1} \\ & xG \le \vec{1} \\ & x_{ikj}\in \{0,1\} \end{align} $$
wobei \(q\in \mathbb{R}^{mn^2}, A=[1, …, 1]^T \in \mathbb{R}^{mn}, G=[1, …, 1]^T \in \mathbb{R}^n\). Es ist \(\operatorname{vec}\) der Vektorisierungsoperator, der Matrizen zue Vektoren ummodelliert. Die Matrizen und Vektoren sind definiert als
$$\begin{align} q & = \operatorname{vec}(Q) ~~~~(Q)_{ikj}=kp_{ij} \\ x & = \begin{bmatrix} x_{111} & \cdots & x_{11n} \\ \vdots & \ddots & \vdots \\ x_{311} & \cdots & x_{31n}\\ x_{121} & \cdots & x_{12n} \\ \vdots & \ddots & \vdots\\ x_{3n1} & \cdots & x_{3nn} \end{bmatrix} \in \mathbb{R}^{mn \times n}\end{align}$$
Beispiel: Lösung
Das Resultat (GLPK, 60 ms) ist gegeben durch die folgende Matrix und das zugehörige Gantt-Diagramm.
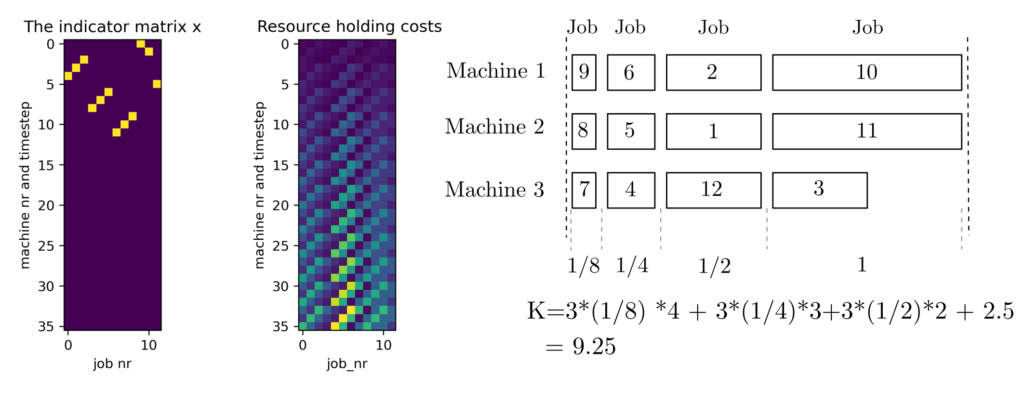
Die Zielfunktion nimmt einen Wert an von 9.25. Man vergleiche die mit dem zufällig und willkürlich gewählten Ablaufplan
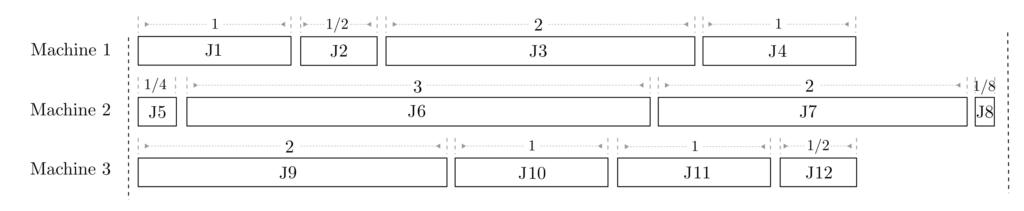
Die damit assoziierten Kosten betragen
$$\begin{align} K =& p_{11}(4)+ p_{12}(3)+p_{13}(2)+p_{14}(1)\\ & +p_{25}(4)+p_{26}(3)+p_{27}(2)+p_{28}(1) \\ & + p_{39}(4)+p_{310}(3)+p_{311}(2)+p_{312}(1) \\& = 4(1+1/4+2)+3(1/2+3+1)+2(2+2+1)+1(1+1/8+1/2) \\ & = 38.125 \end{align} $$
Diese Kosten sind mehr als 4 mal so hoch wie die der optimalen Lösung.
Praktisches
Mit 12 Jobs wäre eine naive Vorgehensweise zur Überprüfung aller Jobanordnungen bereits schwierig. Schon bei nur einer der Maschinen wären \(12!\approx 500 000 000 \) Anordnungen explizit aufzulisten und hinsichtlich ihrer Beschränkungen und ihres Ressourcenverbrauchs zu evaluieren. Bei drei Maschinen sind es mehr als \(10^16\), was die Grenzen normaler Officecomputer bereits sprengt.
Es existieren diverse andere Nebenbedingungen und Zielfunktionen. Typisch sind [1, pp. 14–20]
- Maschinensetups: Einzelmaschine, identische Maschinen, Maschinen mit unterschiedlicher Arbeitsgeschwindigkeit, Unabhängige Maschinen, Flow Job, Job Shop, …
- Nebenbedingungen: Unterbrechbarkeit von Jobs, Abfolgebedingungen, Setupzeiten, Wartezeiten, Deadlines, Jobgruppen, Maschineneinschränkungen, Stapelprozessierung, .…
- Zielfunktionen: Summe der Komplettierungszeiten, Prozessierungsende Einhaltung Deadlines, Verspätungssumme, …
Code & Quellen
Beispielcode: OD_scheduling.py in unserem Tutorialfolder
[1] Pinedo, Michael L. (2016). Scheduling: Theory, Algorithms, and Systems. Berlin, Heidelberg: Springer.
[2] Bansal, N., Srinivasan, A., & Svensson, O. (2016). Lift-and-round to improve weighted completion time on unrelated machines. Proceedings of the forty-eighth annual ACM symposium on Theory of Computing. Association for Computing Machinery, New York, NY, USA, 156–167.
[3] GNU Linear Programming Kit: https://www.gnu.org/software/glpk/
