Anwendung: Statistik & optimal estimation
Definition

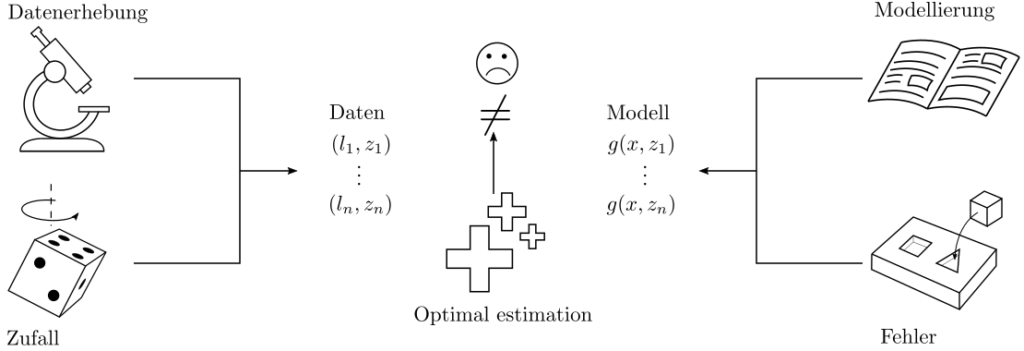
Die mathematische Statistik beschäftigt sich mit Methoden zur Sammlung, Analyse, und Auswertung von Daten. Ziel ist die Ableitung verwertbarer Informationen in Form statistischer Kenngrössen und die optimale Schätzung (optimal estimation) von mit Unsicherheit behafteten Zusammenhängen
Dabei wird die Optimalität der Schätzung von Parametern, unbekannten funktionalen Zusammenhängen, Unsicherheiten, … auf Basis verfügbarer Daten erreicht durch die Maximierung von Wahrscheinlichkeiten. Optimal estimation ist nötig wo auch immer Echtweltkomplexitäten die eindeutige Lösbarkeit eines Problemes behindert.
Beispiel
Die ist beispielsweise der Fall, sobald aus Messdaten Informationen extrahiert werden sollen. Messdaten unterliegen zufälligen und systematischen Schwankungen, die herrühren von Imperfektionen des Messystemes und dynamischen Einflüssen der auf das System einwirkenden Umwelt. Daten sind typischerweise widersprüchlich und müssen verarbeitet werden, bevor sie nützlich sind. Basierend auf einer Messreihe von Werten an den Positionen \(z_k, k=1, …, n\) können diverese Fragestellungen relevant sein:
- Regression. Finde Parameter eines Modelles, die die Beobachtungen bestmöglich erklären.
- Interpolation. Schätze Messwerte an Positionen, an denen gar keine Messungen stattgefunden haben
- Signaltrennung. Zerlege die Messwerte in systematische und zufällige Anteile.
- Unsicherheitsabschätzung. Quantifiziere die Unsicherheiten in den aus Daten abgeleiteten Informationen.
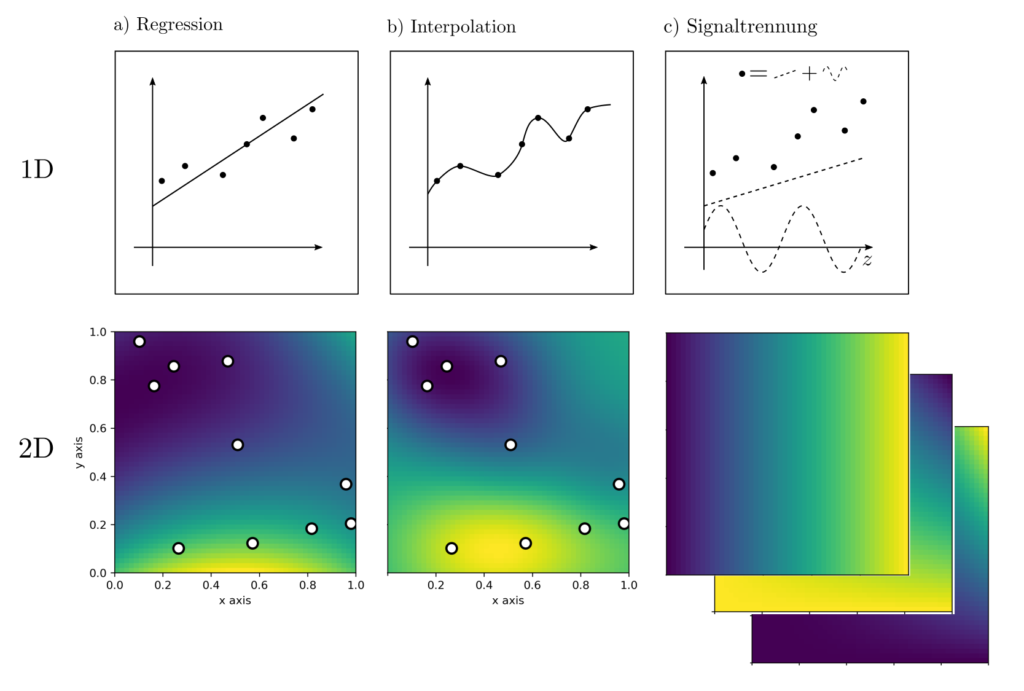
Erklärung Regression
Im Beispiel illustrierend die Regression sind an den Positionen \(z_k, k=1, … ‚n\) die Werte \(l_k, k=1, …, n\) beobachtet worden. Nun sind die Parameter \(x\) so zu wählen, dass Vorhersagen \(g(x,z_k)\) und Beobachtungen \(l_k\) möglichst gut übereinstimmen. Das prädiktive Modell im obig abgebildeten 1D Fall ist die Geradengleichung
$$ g(x,z)=x_1+x_2z$$
welche für jede Stelle \(z\) die Beobachtung \(g(x,z)\) prädiziert. Beliebig komplexere Modelle siend ebenfalls möglich. Sie können die Form \(g(x,z)=\sum_{k=1}^{m_1}x_kg_k(z_1, …, z_{m_2})\) haben mit \(m_1\) Parametern \(x=[x_1, … ‚x_{m_1}\) und \(m_1\) verschiedenen Funktionen \(g_k(z_1, …, z_{m_2})\) abhängend von einer \(m_2\)-dimensionalen Positionsvariable \(z=[z_1, … ‚z_{m_2}]\).
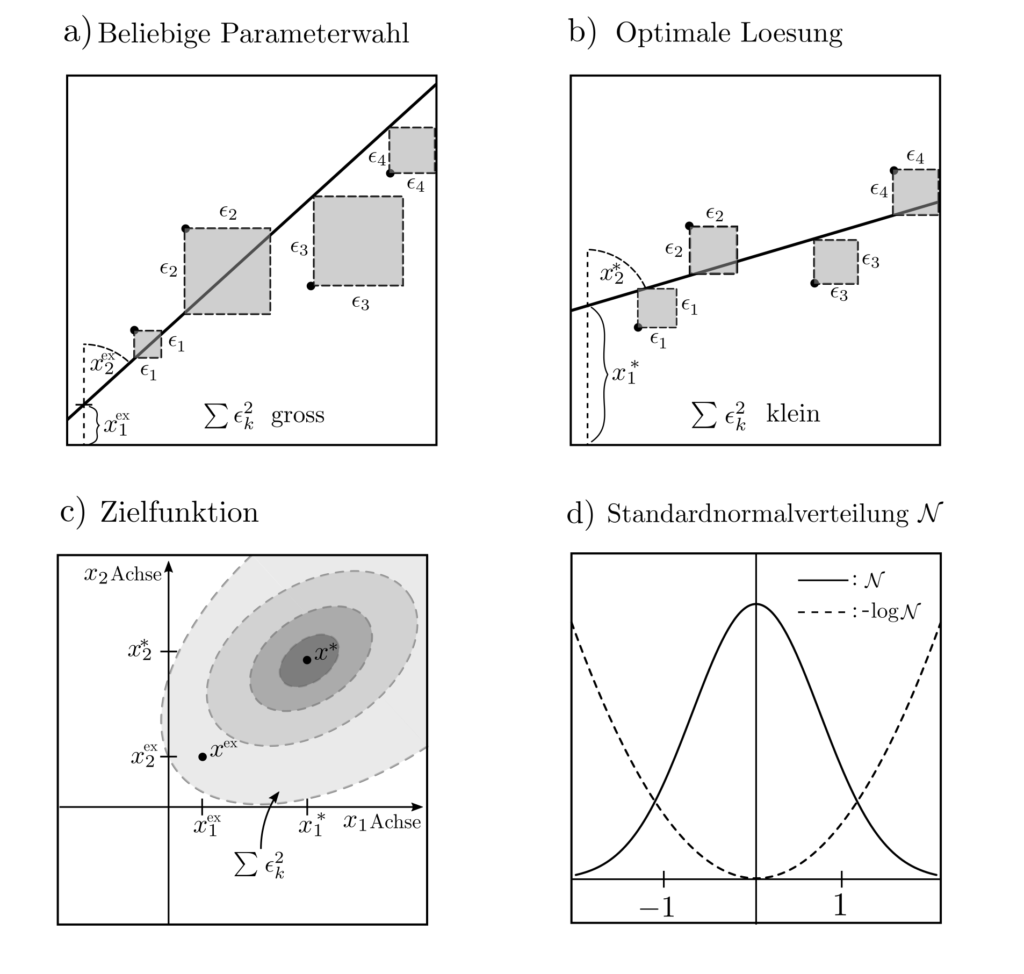
Die Forderung nach einer Wahrscheinlichkeiten maximierenden Wahl des Parametervektors \(x\) lässt sich formalisieren als das Optimierungsproblem
$$ \begin{align} \max_x ~~~& p(l_1, …, l_n, z_1, …, z_n | x_1, x_2) \end{align}$$
wobei die Zielfunktion \(p(l,z|x)\) die Wahrscheinlichkeit einer Beobachtung \(l\) an der Stelle \(z\) angibt, wenn die Parameter zu \(x\) festgelegt sind.
Least squares
Unter der Annahme, dass \(l=x_1+x_2z+\epsilon\) mit \(\epsilon\) standardnormalverteiltem Rauschen, reformuliert sich die Wahrscheinlichkeit zu
$$ p(l_1, …, l_n, z_1, …, z_n|x_1,x_2) = \prod_{k=1}^n p(l_k,z_k|x_1,x_2)= c \exp\left(-\sum_{k=1}^n \frac{1}{2}[l_k-x_1-x_2z_k]^2\right).$$
Die Konstante \(c\) ist irrelevant für die Maximierung der Wahrscheinlichkeiten \(p(l,z|x)\) bzw. die Minimierung von \(-\log p(l,z|x)\) und das folgende Optimierungsproblem resultiert.
$$ \begin{align} \min_{x_1, x_2} ~~~& \sum_{k=1}^n \left[l_k-x_1-x_2z_k\right]^n \\ =\min_{x_1, x_2} ~~~& \|l‑Ax\|_2^2 \\ ~~~& \|l‑Ax\|_2^2=(l‑Ax)^T(l‑Ax) \\ ~~~& A=\begin{bmatrix} 1 & z_1 \\ \vdots & \vdots \\ 1 & z_n \end{bmatrix}^T ~~~ l = \begin{bmatrix}l_1 \\ \vdots \\ l_n\end{bmatrix} \end{align}$$
Es handelt sich um ein einfaches quadratisches Programm ohne Nebenbedingungen, dass sich tatsächlich sogar per Hand lösen lässt zum optimalen \(x^*=(A^TA)^{-1}A^Tl\). Diese Formulierung wist bekannt als least squares problem, da die Quadrate der Diskrepanzen zwischen gemessenen und prädizierten Werten minimiert werden.
Andere Aufgabenstellungen
Auch Interpolation, Signaltrennung, und Unsicherheitsabschätzungen können als Optimierungsprobleme formuliert werden.
$$\begin{align} \text{Interpolation } \min_x ~~~& \|x\|_{\mathcal{H}_2}^2 \\ \text{s.t.} ~~~&Ax=l, x\in \mathcal{H}_2\end{align}$$
$$\begin{align} \text{Signaltrennung } \min_x ~~~&
\|Ax‑l\|_{\mathcal{H}_1}^2+\|x\|_{\mathcal{H}_2}^2 \\ \text{s.t.} ~~~& x\in
\mathcal{H}_2\end{align}$$
$$\begin{align} \text{Unsicherheitsabschätzung } \min_{P,q,r,\tau_1, … ‚\tau_k} ~~~& \langle \Sigma, P\rangle_F+ 2q^T\mu+r\\ \text{s.t.} ~~~& \begin{bmatrix} P & q \\ q^T & r\end{bmatrix} \succeq \tau_i\begin{bmatrix} 0 & a_i/2 \\ a_i^T/2 & ‑b_i \end{bmatrix} \\ & \begin{bmatrix} P & q \\ q^T & r \end{bmatrix} \succeq 0\end{align}$$
Details zur genaueren Bedeutung der quadratischen und semidefiniten Programme sind auf den nachfolgenden Unterseiten zu finden.
Lösungsverfahren
Ist die Anzahl an ins Modell zu integrierenden Daten nicht überbordend gross, so können die Optimierungsprobleme mit öffentlich verfügbaren open-source solvern gelöst werden. Dies ist der Regelfall. Sind jedoch mehrere Hunderttausend oder Millionen Datenpunkte gegeben, dann kann es zu numerischen Komplikationen kommen, die durch intelligentes Ausnutzen zugrundeliegender Problemstrukturen veringert werden.
Um die Verarbeitung riesiger Korrelationsmatrizen mit \(n^2\) Einträgen ( \(n = \) Anzahl Datenpunkte) zu vermeiden, bedient man sich der Tensorzerlegung und numerischer Inversion. Das aus dem Machine learning bekannte stochastic gradient descent umgeht die bei der gesamtheitlichen Datenauswertung auftretenden riesigen Matrizen ebenfalls, indem es die Daten sequentiell verarbeitet. Diese Strategien sind selten nötig, wenn es um Zeitreihen, Audiodaten oder punktuell erhobene Messungen geht, aber unerlässlich, wenn automatisiert generierte multidimensionale Daten z.B. von Kameras oder Radainstrumenten verarbeitet werden müssen.
Anwendungen
Jedes praxisrelevante Problem involviert unbekannte Grössen und Zusamenhänge, weshalb Methoden der Statistik und des optimal estimation mittlerweile überall anzutreffen sind. Anwendungen umfassen die optimale Schätzung von Reisedauern, Hauspreisen, Erzgehalten, Materialeigenschaften, Gebäudedeformationen, Flugbahnen und chemischen Zusammesetzungenen ferner Planeten. Weiterhin die Analyse von Gewinnwahrscheinlichkeiten im Sport oder der Ausfallwahrscheinlichkeit von Bauteilen, die Aufspaltung von Messdaten in Signal und Rauschen, die Identifikation von Objekten in Bildern und die Modellbildung für die Ausbreitung von Krankheiten oder politischen Meinungen. Mehr Anwendungen sind in dieser Liste zu finden.
Optimal estimation ist die Antwort auf die allgegenwärtige Anwesenheit von Daten und Modellunsicherheiten.
Praktisches
Die Hauptschwierigkeit beim Aufstellen von optimal estimation Problemen mit Echtwelthintergrund besteht in der Frage, wie die zufälligen Anteile in den Daten und Modellen dargestellt werden können. Mindestens muss dazu auf Wahrscheinlichkeitsrechnung zurückgegriffen werden und die stochastische Modellierung von Zufallseffekten erfordert Erfahrungen mit auf verschiedene Situationen zugeschnittenen Wahrscheinlichkeitsverteilungen, mehr dazu hier.
In vielen Fällen kann die optimale Schätzung von parametern oder Funktionswerten auf ein least-squares Problem zurückgeführt und sogar händisch gelöst werden. Sind jedoch nichtnormalverteile Grössen involviert, so können die zu maximierenden wahrscheinlichkeiten schnell komplizierte Gestalt annehmen und dedizierte Optimierungsalgorithmen sind gefordert.
Code
Beispielcode: OE_interpolation_regression.py , OE_simulation_support_funs.py in unserem Tutorialfolder
