Optimal estimation : Abschätzung von Fehlerwahrscheinlichkeiten
Problembeschreibung
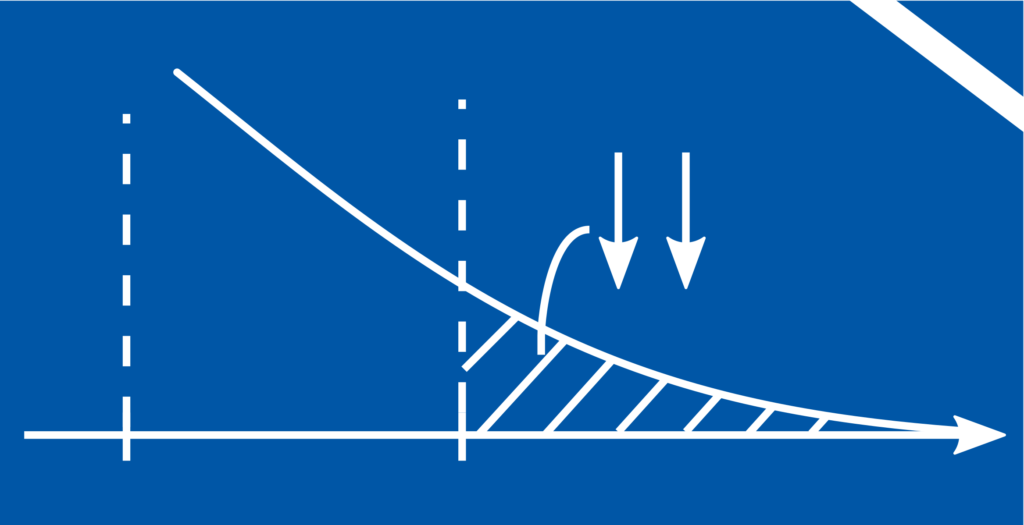
Sind Produktions‑, Entstehungs‑, oder Messprozesse von Unsicherheiten mit bekannter Wahrscheinlichkeitsverteilung geprägt, so können die Wahrscheinlichkeiten \(P(X\in C)\)direkt berechnet werden.
Dabei beschreibt \(P(X\in X)\) die Wahrscheinlichkeit, dass Produkt, Grösse, oder Messung \(X\) im Bereich \(C\subset \mathbb{R}\) annimmt. Die Analyse solcher Wahrscheinlichkeiten ist ein wichtiges diagnostisches Werkzeug zur systematischen Beurteilung von Entscheidungen in unsicheren Situationen.
Problemillustration
Werden beispielsweise Bauteile gefertigt, deren Länge zwecks sicherer Verwendung im Intervall \([a,b]\) liegen müssen, dann stellen die durch Zufälligkeiten im Produktionsprozess hervorgerufenen Variationen der Bauteillänge ein Problem dar. Es sind die Wahrscheinlichkeiten zu untersuchen, dass
- Ein Bauteil mit fehlerhafter Länge \(X\in C, C=\mathbb{R}\setminus [a,b]\) gefertigt wird
- durch Messunsicherheit ein korrekt gefertigtes Bauteil als fehlerhaft deklariert wird (\(\alpha\)-Fehler)
- durch Messunsicherheiten ein fehlerhaft gefertigtes Bauteil als korrekt deklariert wird (\(\beta\)-Fehler).
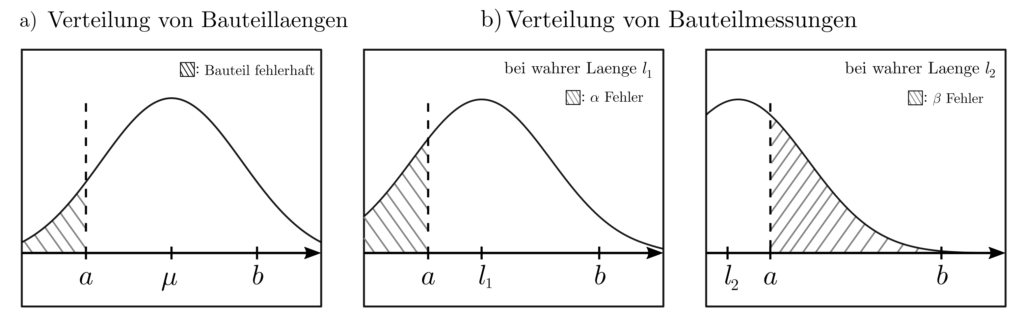
Ist etwa \(X\) normalverteilt mit Erwartungswert \(\mu\) und Standardabweichung \(\sigma\), dann kann die Wahrscheinlichkeit \(P(x\in C)\) berechnet werden zu
$$P(X \le a) + P(X\ge b)= \int_{-\infty}^a p(x)dx + \int_{b}^{\infty} p(x)dx = 1-\int_a^b p(x)dx=1-(\Phi(b)-\Phi(a)).$$
Dabei ist \(\Phi(x)\) die kumulative Wahrscheinlichkeitsverteilung von \(X\) und kann in mathematischen Tabellenwerken nachgeschlagen werden. Dank der 1‑dimensionalität dieses beispielhaften Fehlerabschätzungsproblemes und der genauen Kenntnis der Wahrscheinlichkeitsverteilung ist das Problem demnach mit einfachen Methoden lösbar.
Chebychev Ungleichung : Idee
In realen Anwendungen sind Wahrscheinlichkeitsverteilungen jedoch typischerweise sowohl hochdimensional als auch unbekannt und nur durch deskriptive statistische Kenngrössen wie empirische Mittelwerte und Varianzen beschrieben.
Dennoch können auch in diesem Fall worst-case Wahrscheinlichkeiten \(P(X\in C)\) berechnet werden, indem über mit den Beobachtungen \(E[X]=\mu \in \mathbb{R}^n\) und \(E[XX^T]=\Sigma \in \mathbb{R}^{n\times n}\) konsistente Wahrscheinlichkeitsverteilungen minimiert wird. So kann quantifiziert werden, mit welcher Wahrscheinlichkeit Bauteile qualitativen Anforderungen nicht entsprechen, natürlich entstandene Objekte atypische Eigenschaften aufweisen, oder Messungen grob falsche Beobachtungen hervorbringen.
Chebychev Ungleichung : Optimierungsformulierung
Das Problem lässt sich formulieren als [1, p. 377]
$$ \begin{align} \min_{P,q,r} ~~~& \operatorname{tr} (\Sigma P) + 2 \mu^Tq+r \\ \text{s.t.} ~~~&x^TPx+q^Tx+r \ge 0 ~~\forall x \in \mathbb{R}^n \\ ~~~& x^TPx+q^Tx+r‑1 \ge 0 ~~ \forall x \in C \end{align}$$
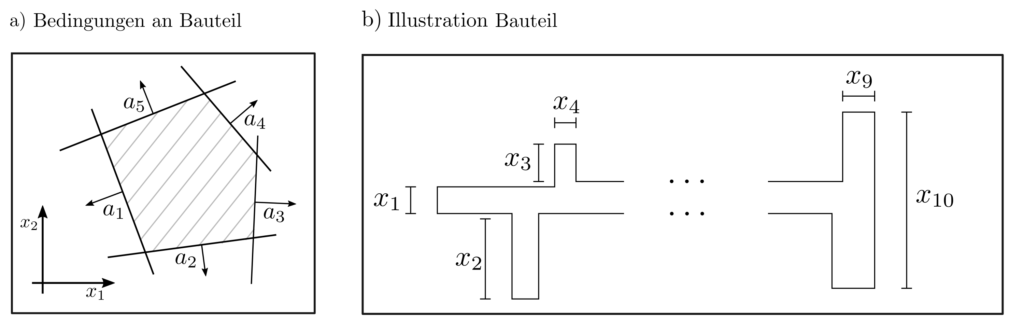
wobei \(\Sigma\) und \(\mu\) die Problemdaten sind und die beiden Ungleichungen garantieren, dass der Wert des Optimierungsproblemes eine obere Schranke ist für \(P(X\in X)\). Handelt es sich bei \(C\) um das äussere eine Polyhedrons \(M\) definiert durch die \(n_c\) Ungleichungen \(a_k^Tz \ge b_k, k=1, …, n_c\), so lassen sich die unendlich vielen Ungleichungen im obigen Optimierungsproblem in eine Forderung nach der Semidefinitheit von Matrizen umwandeln. Das äquivalente semidefinite Programm ist dann [1, p. 377]
$$ \begin{align} \min_{P,q,r, \lambda} ~~~& \operatorname{tr} (\Sigma P) + 2
\mu^Tq+r \\ \text{s.t.} ~~~&\begin{bmatrix}P & q\\ q^T & r\end{bmatrix} \succeq 0 \\ ~~~& \begin{bmatrix} P & q \\ q^T & r‑1\end{bmatrix} \succeq \lambda_k \begin{bmatrix} 0 & a_k/2 \\ a_k^T/2 & ‑b_k \end{bmatrix} ~~~~ k=1, …, n_c \\ ~~~& \lambda_k \ge 0 ~~~~k=1, .…, n_c \end{align}$$
Chebychev Ungleichung : Anwendung
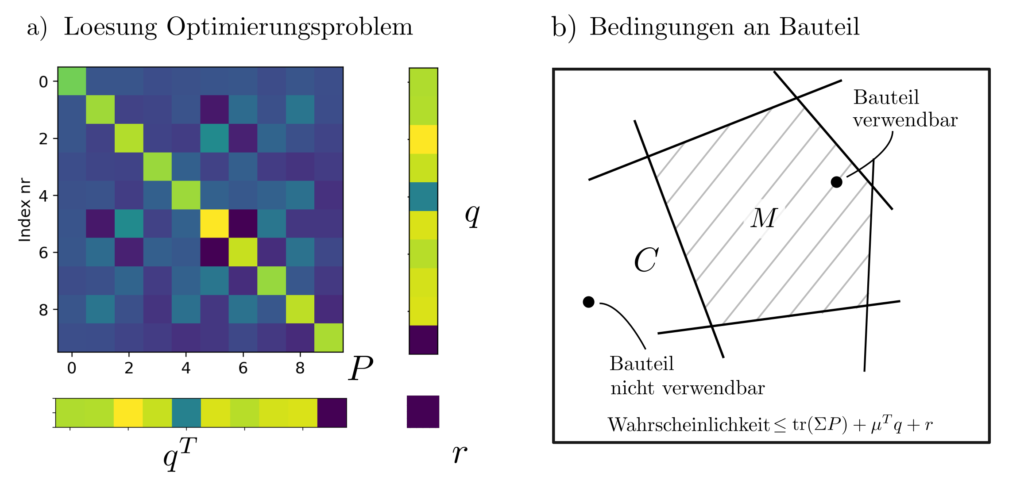
Das nachfolgende Bild illustriert eine beispielhafte Lösung des folgenden Problemes. Eine Maschinenkomponente mit zufälligen Längencharakteristiken \(X_1, …, X_{10}\) werde gefertigt. Die Erwartungswerte und Kovarianzen der Längencharaketeristiken sind bekannt; z.B. durch Messung einer Testmenge von Komponenten. Eine Komponente ist nur dann verwendbar zum Einbau in die übergeordnete Maschine, wenn sie die 20 Bedingungen
$ a_k^T x \le b_k ~~~~ k=1, …, 20$
an die Längen erfüllt. Dieses Problem ist leicht lösbar mit CVXPY [2].
Die nachfolgenden Abbildungen zeigen die optimalen Matrizen \(P\), Vektoren \(q\) und Skalare \(r\), sodass \(\operatorname{tr}(\Sigma P) + 2 \mu^Tq+r \) gerade die kleinste obere Schranke ist für \(P(X\in C)\). Mit den dort abgebildeten \(P,q,r, \lambda\) gilt \(P(X\in C)\le 0.4\). Mehr Informationen zu diesem sogenannten Momentenproblem sind zu finden in [3, pp. 469–509].
Integration von Zusatzinformationen
Ist mehr bekannt über die zugrundeliegende Wahrscheinlichkeitsverteilung als nur die Erwartungswerte \(E[X]\) und \(E[XX^T]\), dann können diese Informationen zur Verbesserung der Fehlerabschätzung verwendet werden und erlauben die Lösung weiterer Probleme. Die Optimierung über Wahrscheinlichkeitsverteilungen kann verbessert werden durch Kenntnis der
- Schranken der Momente \(M_k=E[X^k], ~~ k=1, …, n\). Da die Hankel-Matrix $$\begin{bmatrix} M_0 & M_1 & M_2 & \cdots \\ M_1 & M_2 & \cdots & \\ M_2 & \vdots & \ddots & \\ \vdots & & & \end{bmatrix} \succeq 0$$ der Momente \(M_k\) einer Wahrscheinlichkeitsverteilung positiv semidefinit sein muss, kann eine Optimierung über Momente als SDP geschrieben werden [1, p. 171].
- marginale Wahrscheinlichkeitsverteilungen \(\bar{p}=\{\bar{p}_1, …, \bar{p}_n\}\) und \( \bar{q}=\{\bar{q}_1, …, \bar{q}_m\}\) der Zufallsvariablen \(X_1\) und \(X_2\). Da die multivariate Verteilung definiert wird durch die Matrix $$P=\begin{bmatrix} p_{11} & \cdots & p_{1n}\\ \vdots & \ddots & \vdots\\ p_{m1} & \cdots & p_{mn}\end{bmatrix}$$ von Wahrscheinlichkeiten \(p_{ij}=P(X_1=x_i,X_2=x_j)\ge 0\), lassen sich die Optimierungen über multivariate Wahrscheinlichkeitsverteilungen als LP mit Nebenbedingungen \(\sum_{j=1}^np_{ij}=\bar{q}_i\) und \(\sum_{i=1}^m p_{ij}=\bar{p}_j\) schreiben.
- kumulantengenerierenden Funktion \(\log E\left[ \exp(\lambda^Tx)\right]\) der Wahrscheinlichkeitsverteilung von \(X\). Je nach genauer Form dieser Funktion ergibt sich durch die Chernoff-Ungleichung [1, p. 380]$$ \begin{align}P(X\in C) \le e^q ~~~~&~~~~ C=\{x: Ax \le b\} \\q= \min_{\lambda u} ~~~& b^Tu+\log E[\exp(\lambda^T X)] \\ \text{s.t.} ~~~&u \ge 0 ~~~ A^Tu+\lambda=0 \end{align}$$ ein LP, QP, SDP, oder ein nicht mit konventionellen Methoden lösbares konvexes Optimierungsproblem zur Beschränkung der Auftrittswahrscheinlichkeiten eines Ereignisses.
Anwendungen und Praktisches
Fehlerabschätzungen der oben beschriebenen Art sind besonders bei der Risikobeschränkung hilfreich. Müssen Aussagen über nur hinsichtlich ihrer Wahrscheinlichkeitsverteilung bekannte Grössen getroffen werden oder unsichere Messungen in definitive Entscheidungen umgewandelt, dann können diese Methoden einen echten Mehrwert darstellen.
Die Risikoschranken hängen ab nicht von der genauen Wahrscheinlichkeitsverteilung sondern von der Gesamtkonfiguration des Problemes. Dieser Zusammenhang kann genutzt werden, um eine Problemkonfiguration zu finden, welche die Risikoschranken auf ein akzeptables Mass absenkt.
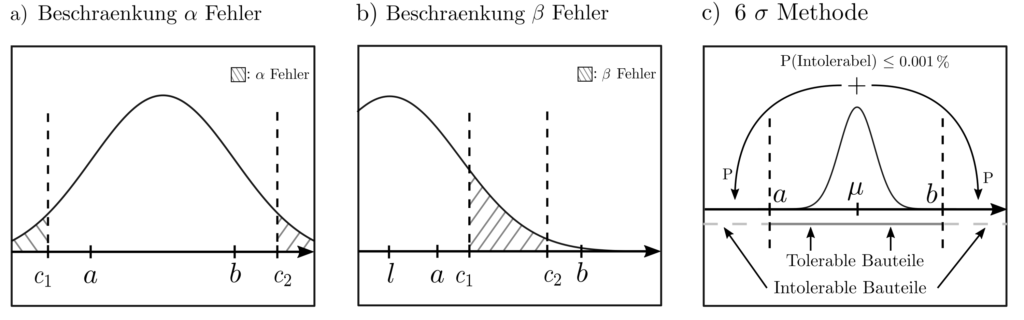
Das etablierte 6 \(\sigma\) Kriterium zur Definition statisischer Qualitätsziele im Produktionsmanagement ist den obigen Methoden ähnlich, wenn auch mathematisch weniger involviert. Der durch höhere Komplexität und höheren stochastischen Modellierungsaufwand erkaufte Gewinn besteht in schärferen, weniger konservativen Wahrscheinlichkeitsabschätzungen.
Code & Quellen
Beispielcode: OE_bounding_probabilities.py in unserem Tutorialfolder
[1] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.
[2] Diamond S., & Boyd S., (2016). CVXPY: A Python-embedded modeling language for convex optimization. Journal of Machine Learning Research, 17(83), 1–5.
[3] Wolkowicz, H., Saigal, R., & Vandenberghe, L. (2012). Handbook of Semidefinite Programming: Theory, Algorithms, and Applications. Berlin Heidelberg: Springer Science & Business Media.
