Mathematische Optimierung: Methoden
Numerik
Ist ein Optimierungsproblem \( \min f(x), x \in D\) formuliert, so muss es noch immer gelöst werden. Die genaue Funktionsweise dieses Lösungsprozesses ist abhängig von der Struktur der Funktion \( f(x) \) und des Suchraumes \( D\). Sind beide nichtlinear, so ist das Problem unter Umständen nicht mit derzeitigen Methoden lösbar. In jedem Fall liegt die Lösung von Optimierungsproblemen in der Domäne der Numerik — derjenigen mathematischen Disziplin, die sich mit der Konstruktion von Algorithmen zur Lösung mathematischer Probleme beschäftigt.
Die Entwicklung numerischer Algorithmen ist eine schwierige Angelegenheit, die Abwägungen erfordert bezüglich Rundungsfehlern, Rechenintensität, Speicherplatzbedarf, Laufzeiten, Korrektheit, und Zuverlässigkeit des vom Algorithmus ausgegebenen Lösungsvorschlages. Typischerweise verarbeitet ein solcher Algorithmus die Problemdaten \(f\) und \(D\) nach einem nichtlinearen und iterativen Schema, bei dessen Entwicklung einiges an Potential für Fehler besteht.
Klassen Optimierungsprobleme
Glücklicherweise sind für bestimmte archetypische Klassen von Funktionen \(f\) und Suchräumen \(D\) bereits zuverlässige Lösungsalgorithmen entwickelt und als Computerprogramm implementiert worden. Konsequenterweise wird ein Optimierungsproblem am komfortablesten gelöst, wenn es als Instanz einer Klasse von Optimierungsproblemen gelöst werden kann, für die Lösungsalgorithmen zur Verfügung stehen. Dazu gehören die folgenden Konfigurationen.
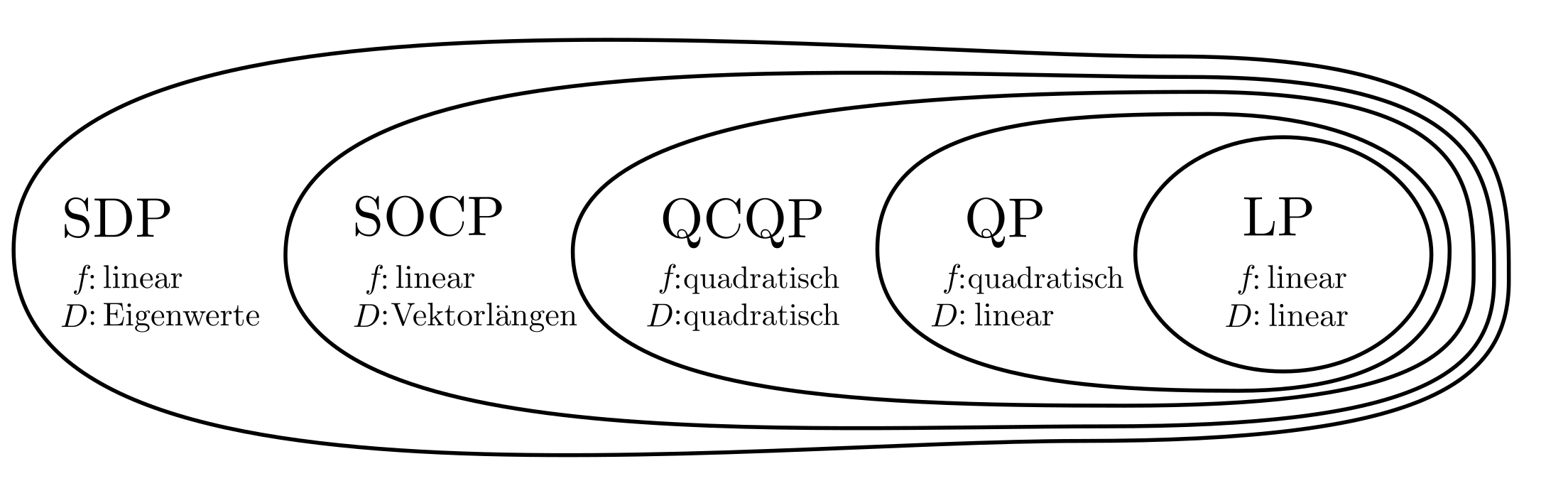
Zusammenhang Klassen
Ist demnach das Optimierungsproblem
$$ \begin{align} \min_x ~~~&f(x) \\ \text{s.t.} ~~~&x \in D \end{align}$$
formulierbar als LP, QP, QCQP, SOCP, oder SDP und somit als Problem involvierende bestimmte Polynome der Ordnung 2, dann ist es zuverlässig lösbar mit beschränktem Rechenaufwand. Weitere Problemklassen existieren z.B. unter den Namen Geometric Programming [1, p. 160], log-log convex Programming [2] oder Maxdet Problem [3], doch die obigen Klassen decken bereits ein breites Spektrum ab.
Weiterhin von Interesse ist das sogenannte dynamic programming, das sich mit der Optimierung von Abfolgen von Entscheidungen beschäftigt eine grosse praktische Bedeutung in der Optimierung operationeller Abläufe besitzt. Für viele der obigen Klassen kann auch die weitere Nebenbedingung \( x \in Z\) eingefügt werden, i.e. dass \(x\) ganzzahlig sein soll. Die Berücksichtigung solcher Bedingungen kann sinnvoll sein, wenn es sich bei \(x\) um diskrete unteilbare Einheiten wie z.B. logische ja-nein Entscheidungen handelt. Die Lösungsalgorithmen werden jedoch ungleich unzuverlässiger und es können keine garantien mehr ausgesprochen werden. Das problem ist nicht konvex und NP-schwer genau so wie die sogenannte black-box optimization zur Optimierung von Funktionen ohne bekannte Struktur.
Ausblick
Auf den untergeordneten Seiten finden sich Informationen zu LP, QP, QCQP, SOCP, SDP sowie deren gemisch-ganzzahligen Varianten, zum dynamic programming und zur black-box optimization.
Quellen
[1] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.
[2] Agrawal, A., Diamond, S., & Boyd, S. (2019). Disciplined geometric programming. Optimization Letters, 13(5), 961–976.
[3] Vandenberghe, L., Boyd, S., & Wu, S. (1998). Determinant Maximization with Linear Matrix Inequality Constraints. SIAM Journal on Matrix Analysis and Applications 1998 19:2, 499–533
