Methoden: Linear programming
Definition
Unter linear programming (LP) sind sämtliche Optimierungsprobleme zusammengefasst, deren Zielfunktion und Nebenbedinungen linearer Natur sind. Es handelt sich um die einfachste Klasse von Optimierungsproblemen, die numerische Lösungsansätze erfordern. Sie lassen sich allesamt schreiben in der Form
$$ \begin{align} \min_x ~~~& \langle c,x\rangle \\ \text{s.t.} ~~~&Ax=b \\ ~~~& Gx\ge h \end{align}$$
in der Optimierungsvariablen \(x\). Hierbei sind \(x, c, b, h\) Vektoren und \(A, G\) sind Matrizen. Das obige Problem in detaillierter Schreibweise lautet demnach wie folgt.
- Finde die Variablen \(x_1, …, x_n\) sodass \(\langle c,x\rangle = c_1x_1 +, … , +c_nx_n\) minimal wird
- Dabei soll gelten:
- \(a_{k1} x_1 + , …, + a_{kn}x_n =b_k ~~~~k=1, …, m_1\)
- \(g_{k1} x_1 + , …, + g_{kn}x_n \ge h_k ~~~~k=1, …, m_2\)
Das Problem besteht aus einer zu minimierenden Summe \(\langle c,x\rangle\), \(m_1\) Gleichungen, und \(m_2\) Ungleichungen. Alle Terme sind linear in der Optimierungsvariablen \(x\), daher der Name “linear programming”.
Beispiel
LP beinhaltet archetypische wirtschaftliche Produktionsprobleme wie etwa die Produktionsplanerstellung [1, pp. 14–16]. Sind etwa \(x_1, x_2\) die Mengen zweier Produkte mit Produktionskosten \(c_1, c_2\), so lässt sich das Optimierungsproblem
$$ \begin{align} \min_x ~~~& c_1 x_1 + c_2 x_2 \\ \text{s.t.} ~~~&x_1 + x_2 =2 \\ ~~~& x_1 \ge 0 ~~~ x_2 \ge 0 \end{align}$$
interpretieren als die Anweisung, Produktionskosten zu minimieren und einen Gesamtbedarf von 2 zu decken. Dabei seien negative Produktionsmengen nicht erlaubt. Erweiterungen dieses beispieles auf mehrere Produkte, Mindestbedarfe, und Ressourcenverbrauchsbeschränkungen sind problemlos möglich.
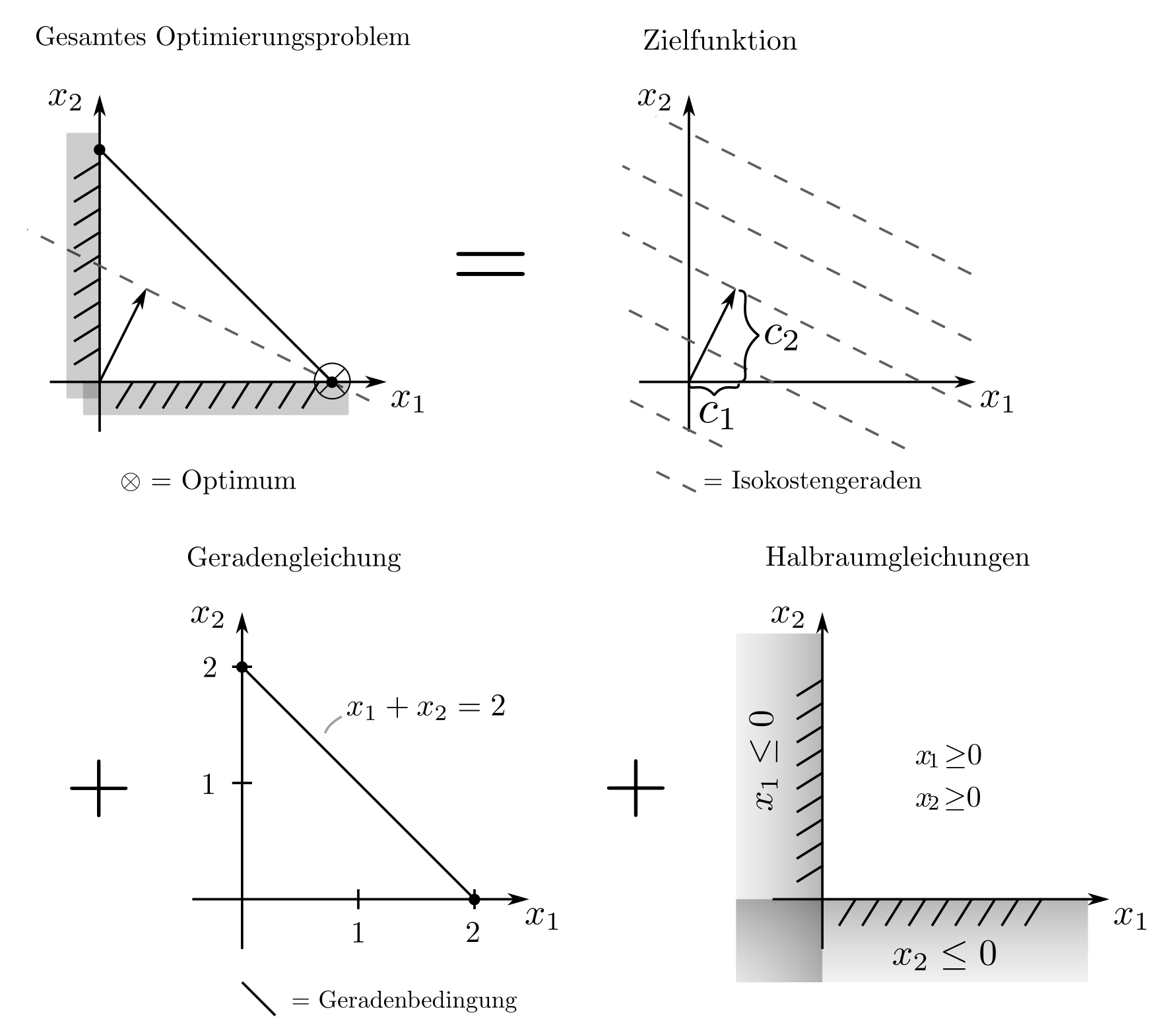
Geometrisches
Das obige Beispiel hat eine klare geometrische Interpretation als Bestimmung eines zweidimensionalen Punktes \(x = [x_1,x_2]\), der hinsichtlich seiner Lage durch einige Geraden beschränkt ist.
Das Optimum wird an dem Eckpunkt der zulässigen Menge erreicht, durch den die minimale Kostenäquivalenzgerade verläuft. Bei hochdimensionalen Problemen werden aus 2‑dimensionalen Vektoren n‑dimensionale Vektoren, Geradengleichungen werden zu Hyperebenengleichungen, und die Ungleichungen definieren Halbräume. Die grundlegenden geometrischen Eigenschaften und Interpretationen bleiben erhalten.
Anwendungen
Die Anwendungsmöglichkeiten linearer Programmierung erstrecken sich weit über die Produktionsplanung hinaus. Sie beinhalten Probleme aus den bereichen Logistik, Transport- und Routenplanung, Maschinenbelegungsplanung, Inventarkontrolle, Diätendesign, Materialfluss, Fabriklayout, Stochastische Ungleichungen, Bildqualitätsoptimierung, Datenkompression, Robuste Approximation, Spieltheorie, und Logik. Details sind hier zu finden. Je nach Anwendung repräsentiert \(\langle c,x\rangle\) monetäre Kosten, negativen Gewinn, Zeitdauern, Maximalabweichungen, Wahrscheinlichkeiten, oder schwer interpretierbare Hilfsgrössen. Die Repräsentationen dieser Probleme als LP sind oft nicht offensichtlich.
Lösungsverfahren
Lineare Programme sind historisch gesehen die ersten praxisrelevanten hochdimensionalen Optimierungsprobleme, die sich zuverlässig lösen liessen. Im Zusammenhang mit Planungsproblemen der US Air Force nach dem 2. Weltkrieg wurde von Dantzig die sogenannte Simplex-Methode entwickelt, deren Weiterentwicklung und Nutzung für Ressourcenallokationsprobleme Koopmans und Kantorovic zu einem Wirtschaftsnobelpreis verhalf [2, p. 10].
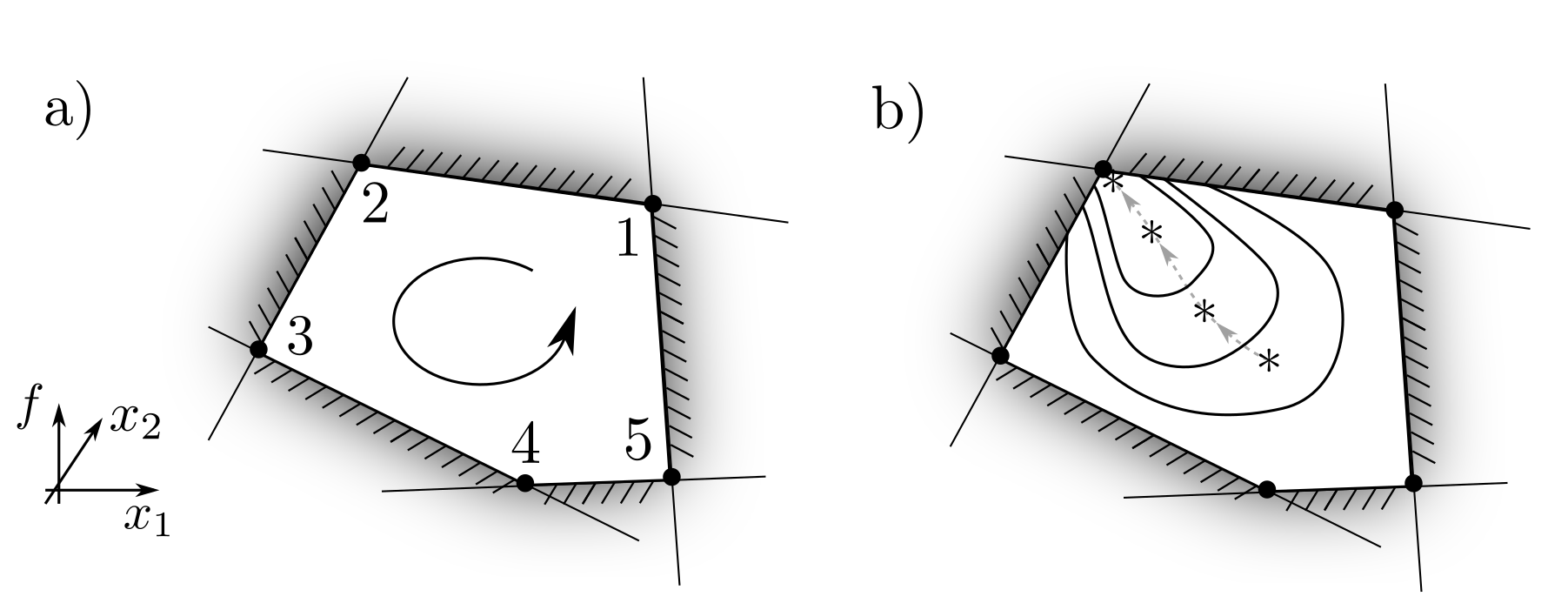
Wie bereits in Abbildung 1 bemerkt und generell beweisbar, befindet sich der optimale Punkt \(x\) eines LP an einem der Eckpunkte der zulössigen dirch Schnitte von Hyperebenen definierten Menge. Enumeration und subsequentielles Testen jedes Eckpunktes führt zur zuverlässigen Identifikation des Optimums [3, p. 72]. Da die Anzahl der Eckpunkte mit der Anzahl der Dimensionen überproportional wachsen kann, ist diese vollständige Enumeration oft teuer und mittlerweile existieren bessere Möglichkeiten; die interior-point methods. Diese Verfahren beruhen darauf, die Ungleichungen durch Barrierefunktionen zu ersetzen, deren Gewicht inkrementell reduziert wird. Dadurch wird eine Folge von Punkten — der zentrale Pfad — generiert, welche zum Optimum konvergiert.
Praktisches
LP mit hunderttausenden Optimierungsvariablen sind heutzutage auch auf handelsüblichen Heimrechnern gut lösbar. Dazu existieren open source Algorithmen wie etwa implementiert im Gnu linear programming kit (GLPK) oder im Google GLOP solver. Dass selbst Excel mittlerweile in der Lage ist, LP zu lösen mag als weiteres Zeugnis gesehen werden, dass LP technische Maturität erreicht hat. Die Herausforderung besteht vor allem in der Formulierung des Optimierungsproblemes selber.
Quellen
[1] Hu, T. C., & Kahng, Andrew B. (2016). Linear and Integer Programming Made Easy. Berlin, Heidelberg: Springer.
[2] Vanderbei, Robert J. (2013). Linear Programming: Foundations and Extensions. USA: Springer US.
[3] Gass, Saul I. (2003). Linear Programming: Methods and Applications. New York: Courier Corporation.
