Methoden: Mixed integer Programming
Definition
Sobald ein Optimierungsproblem Nebenbedingungen betreffend die Ganzzahligkeit von Variablen aufweist, spricht man von einem Integer program. Die Ganzzahligkeitsforderung an eine Variable \(x_1\) wird geschrieben als \(x_1 \in \mathbb{Z}\) wobei \(\mathbb{Z}\) die Menge aller ganzen Zahlen ist.
Sind weiterhin noch andere Nebenbedingungen involviert, so spricht man von einem Mixed integer Program (MIP). Je nach Form der Zielfunktion \(f\) und der zulässigen Menge \(D\) im Optimierungsproblem
$$ \begin{align} \min_x ~~~& f(x) \\ \text{s.t.}
~~~&x \in D \\ ~~~& x_1, …, x_m\in \mathbb{Z} \end{align}$$
von MILP, MIQP, MISDP, usw. Die klassischen Optimierungsprobleme können mit Forderungen nach Ganzzahligkeit angereichert werden, um sie expressiver zu machen.
Beispiel 1
Seien \(x_1, x_2 \) die Mengen zweier Produkte mit Herstellungskosten von respektive \(c_1\) und \(c_2\). Die Bedingungen, dass Ihre Summe den Bedarf von 2 decken soll und \(x_1, x_2\) nur in diskreten Mengen produzierbar sind, lassen sich übersetzen in das Optimierungsproblem
$$ \begin{align} \min_x ~~~& c_1x_1+c_2x_2 \\ \text{s.t.}
~~~&x_1 \ge 0 ~~~ x_2 \ge 0 \\ ~~~& x_1+x_2=2\\~~~& x_1, x_2\in \mathbb{Z} \end{align}$$
in der Optimierungsvariablen \(x\). Diese Variation des archetypischen Produktionsplanbeispieles ist nahezu trivial: Die zulässige Menge besteht aus den drei Elementen \([0,2], [1,1], [2,0]\) und lässt sich leicht hinsichtlich ihres maximums untersuchen. In dem Fall hat die Inklusion der Ganzzahligkeit das Optimierungsproblem einfacher gemacht. Doch das ist bei weitem nicht immer so.
Beispiel 2
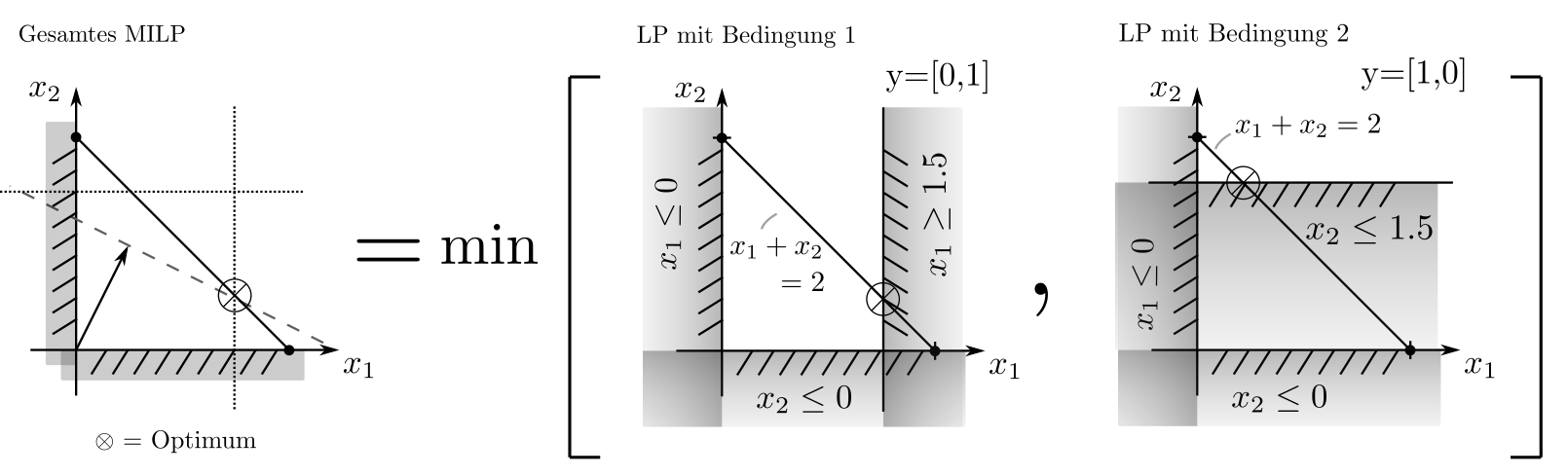
Ein weiteres Beispiel zeigt, dass Ganzzahligkeit eine unerwartet flexible Nebenbedingung ist. Sei die Situation wie in Beispiel 1; allerdings ohne die Bedingungen \(x_1\in \mathbb{Z}, x_2\in \mathbb{Z}\). Stattdessen soll mindestens eine der vertraglichen Bedingungen \(x_1 \le 1.5\) oder \(x_2\ge 1.5\) gewährleistet sein. Dies lässt sich formulieren als MILP
$$ \begin{align} \min_x ~~~& c_1x_1+c_2x_2 \\ \text{s.t.}
~~~&x_1 \ge 0 ~~~ x_2 \ge 0 \\ ~~~& x_1+x_2=2\\~~~& x_1 ‑M_1y_1 \le 1.5 ~~~~~~~~~~~~~~ M_1 \text{ Obergrenze für } x_1 \\ ~~~& ‑x_2 ‑M_2y_2 \le ‑1.5 ~~~~~~ M_2 \text{ Obergrenze für } ‑x_2 \\ ~~~& y_1+y_2=1 ~~~~ y_1,y_2\in \{0,1\} \end{align}$$
in den Optimierungsvariablen \(x\) und \(y\). Dabei ist \(y=[y_1,y_2]\) entweder \([0,1]\) oder \([1,0]\) und indiziert, welche der beiden vertraglichen Nebenbedingungen gewährleistet sein soll.
Anwendungen
Die Forderung nach Ganzzahligkeit ist ein unerwartet flexibles Kriterium. Wie im obigen Beispiel gezeigt, können mit ihrer Hilfe logisch gekoppelte Nebenbedingungen formuliert werden [1, p. 6]. Mit den logischen Atomen UND sowie ODER und deren Kombinationen können ganze Entscheidungsbäume in Optimierungsprobleme eingebettet werden. Ganzzahlige Optimierung stellt daher auch eine Grundlage der Formulierung von Lösbarkeitsproblemen.
Weiterhin sind nichtlineare Terme in Optimierungsproblemen darstellbar als lineare Terme mit Ganzzahligkeitsbedingungen [2, pp. 396–396].
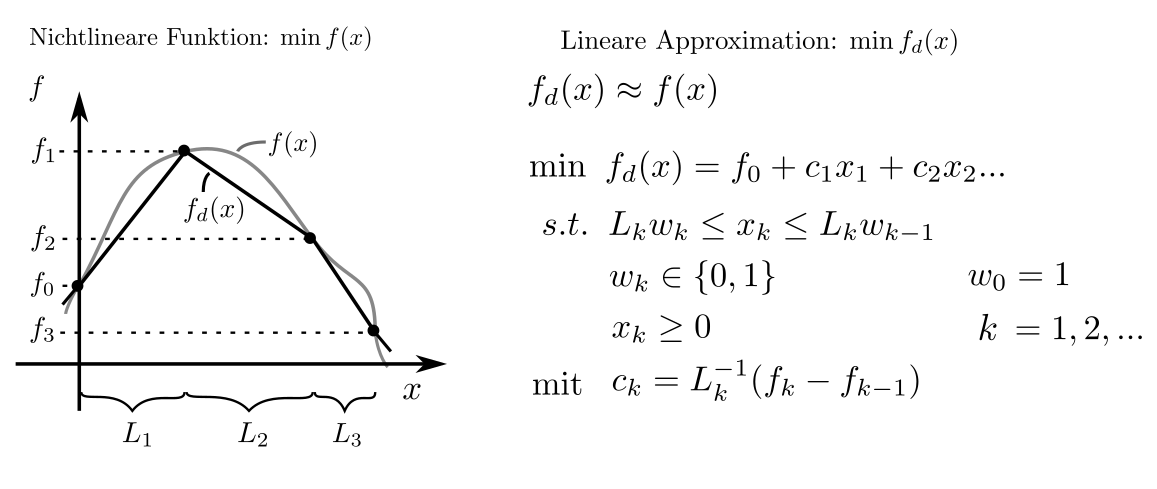
Es ist klar, dass ein Formalismus zur Darstellung und Lösung von Problemen diskreter, logischer, und nichtlinearer Natur viele Anwendungen hat. Sie sind unter anderem zu finden bei optimalen Steuerungsproblemen mit diskreten Inputmöglichkeiten wie etwa der Regelung von bestandsabhängigem Fischereibetrieb, Supermarktkühlketten, Flugzeugsteuerungsinputs, und Kollisionsvermeidung. Ebenso treten sie auf bei optimalen Designproblemen mit diskretem Charakter wie Transportnetzwerkdesign, Fahzeugrouting, Güterflusssteuerung, Fabriklayout, räumlicher Anordnung von Infrastruktur, Testreihenfolge und Experimentendesign, Speicherplatzmanagement, und logischen Machbarkeitsproblemen. Mehr Informationen sind hier zu finden.
Lösungsverfahren
Obwohl ganzzahlige Optimierungsprobleme im Allgemeinen sehr schwierig sind, gibt es exakte Lösungsmethoden wie den branch-and-cut Algorithmus, die in der Praxis hinreichend leistungsfähig erscheinen. Die Lösungsmethoden beruhen auf der Konstruktion einer Baumstruktur von approximativen LP’s mit einer zunehmenden Anzahl an linearen Nebenbedingungen, deren Kombination die Ganzzahligkeitsbedingungen erzwingen [2, pp. 396–413].
Diese Baumstruktur kann effizient durchsucht werden mittels einer Kombination aus Tiefensuche und der Aufgabe derjenigen Baumbestandteile, die nachweislich zu schlechteren Lösungsvorschlägen führen als vorgängig bereits evaluierte. Beispiel für die Implementation eines solchen Lösungsalgorithmus ist das GNU linear programming KIT mit der GLPK_MI Routine [3].
Praktisches
Ganzzahlige Optimierungsprobleme sind nicht immer in angemessener Zeit lösbar. Sie gehören zu den ausdrucksfähigksten aber auch schwersten Problemen, die der Mathematik und Informatik bekannt sind [4]. Von einem empirischen Standpunkt aus gesehen funktionieren sie jedoch häufig gut genug für praktische Probleme, welche wenige Tausend ganzzahlige Variablen nicht überschreiten. Dies ist prmär eine Frage der Problemstruktur.
Einige Problemformulierungen sind einfach zu interpretieren, da sie als Optimierungsvariablen ganzzahlige diskrete Objekte enthalten. Oft jedoch müssen nichtlineare Terme oder logische Konstrukte in Nebenbedingungen übersetzt werden. Dies erfordert Zeit, Erfahrung, und ist nicht immer möglich.
Code & Quellen
Beispielcode: Methods_milp.py in unserem Tutorialfolder
[1] Appa, G. M., Pitsoulis, L., & Williams, H. P. (2006). Handbook on Modelling for Discrete Optimization. Berlin, Heidelberg: Springer.
[2] Vanderbei, Robert J. (2013). Linear Programming: Foundations and Extensions. USA: Springer US.
[3] GNU Linear Programming Kit: https://www.gnu.org/software/glpk/
[4] Padberg, M. (2005). Classical Cuts for Mixed-Integer Programming and Branch-and-Cut. Annals of Operations Research, 139, 321–352.
