Methoden: Quadratic programming und SOCP
Definition

Quadratic programming (QP), quadratically constrained quadratic programming (QCQP) u, und second order cone programming (SOCP) sind Generalisierungen des linear Programming (LP). SIe beinhalten viele Praxisrelevante Probleme inlusive Verallgemeinerungen des Least Squares.
Die lineare Zielfunktion und die linearen Nebenbedingungen des LP werden erweitert zu quadratischen Zielfunktionen und quadratischen Nebenbedingungen. Quadratische Programme haben die Form
$$ \begin{align} (QP)~~~~ & ~~~~~~~~~~& (QCQP)~~~~ &\\ \min_x ~~~& \frac{1}{2} x^TP_0x+\langle c_0,x\rangle& \min_x ~~~& \frac{1}{2} x^TP_0x+\langle c_0,x\rangle \\ \text{s.t.} ~~~&Ax=b & ~~~&Ax=b \\ ~~~& Gx\ge h & ~~~& \frac{1}{2} x^TP_kx+\langle p_k,x\rangle\le h_k ~~~ k=1, …, m_2\end{align}$$
wobei \(x, c_0, c_1, …, c_{m_2}, b, h\) Vektoren und \(P_0, P_1, …, P_{m_2}, A, G\) Matrizen sind. QP ist eine direkte Erweiterung von LP um den quadratischen Term \((1/2) x^TP_0x\) in der Zielfunktion und QCQP erweitert QP um quadratische Terme \((1/2)x^TP_kx\) in den Nebenbedingungen. Sie beinhalten Kreis- und Ellipsoidgleichungen. SOCP untersucht das noch allgemeinere Optimierungsproblem
$$ \begin{align} \min_x ~~~& \langle c, x\rangle \\ \text{s.t.}
~~~&Ax =b \\ ~~~& \|G_k x +h_k\|_2 \le \langle f_k,x\rangle + d_k ~~~ k=1, …, m_2 \end{align}$$
in der Optimierungsvariablen x. Dabei sind \(x, c, b, f_1, …, f_{m_2}, h_1, …, h_{m_2}\) Vektoren, \(A, G_1, …, G_{m_2}\) Matrizen, und \(d_1, …, d_{m_2}\) Skalare.
Beispiel
SOCP erlaubt die Lösung linearer Programme, deren Bedingungen stochastischer Natur sind. Seien zwei Produkte in solchen Mengen \(x_1, x_2\) herzustellen, dass der Bedarf \(b\) unter Aufwendung minimaler Produktionskosten \(c_1x_1 +c_2x_2\) gedeckt werde. Sei nun weiterhin der Produktionsprozess mit Unsicherheiten behaftet, sodass nur Teile \(a_1x_1, a_2x_2\) des Herstellungsoutputs nutzbar sind. Sind nun \([a_1,a_2]\) zufällig, so macht es Sinn, die Einhaltung der Bedarfsdeckung nicht mehr absolut aber mit hoher Wahrscheinlichkeit \(\eta\) zu fordern. Ist \(a=[a_1,a_2]\) normalverteilt mit Erwartungswert \(\bar{a}=[\bar{a}_1, \bar{a}_2]\) und Kovarianzmatrix \(\Sigma\), so gilt
$$ \begin{align} P(a^Tx \ge b)\ge \eta & \Leftrightarrow \phi^{-1}(\eta) \|\Sigma^{1/2} x \|_2 \le \bar{a}^Tx — b \end{align} $$
wobei \(P(\cdot)\) für die Wahrscheinlichkeit des umklammerten Ausdruckes steht und \(\phi^{-1}\) die inverse der kumulativen Normalverteilungsfunktion ist. Das zugehörige SOCP
$$ \begin{align} \min_x ~~~& c_1x_1 + c_2x_2 \\ \text{s.t.}
~~~&x_1 \ge 0 ~~~ x_2 \ge 0 \\ ~~~& \phi^{-1}(\eta)\|\Sigma^{1/2}x\|_2 \le \bar{a}^Tx‑b \end{align}$$
formuliert eine Kostenminimierung bei gleichzeitiger Bedarfsdeckungswahrscheinlichkeit von \(\eta\) % [1, p.158]. Die nachfolgende Abbildung illustriert dies für den Fall \(\bar{a}=[0.7, 0.7], \Sigma=0.1 I \) und \(\eta=90\%\); die restlichen Parameter sind wie im Beispiel zum LP.
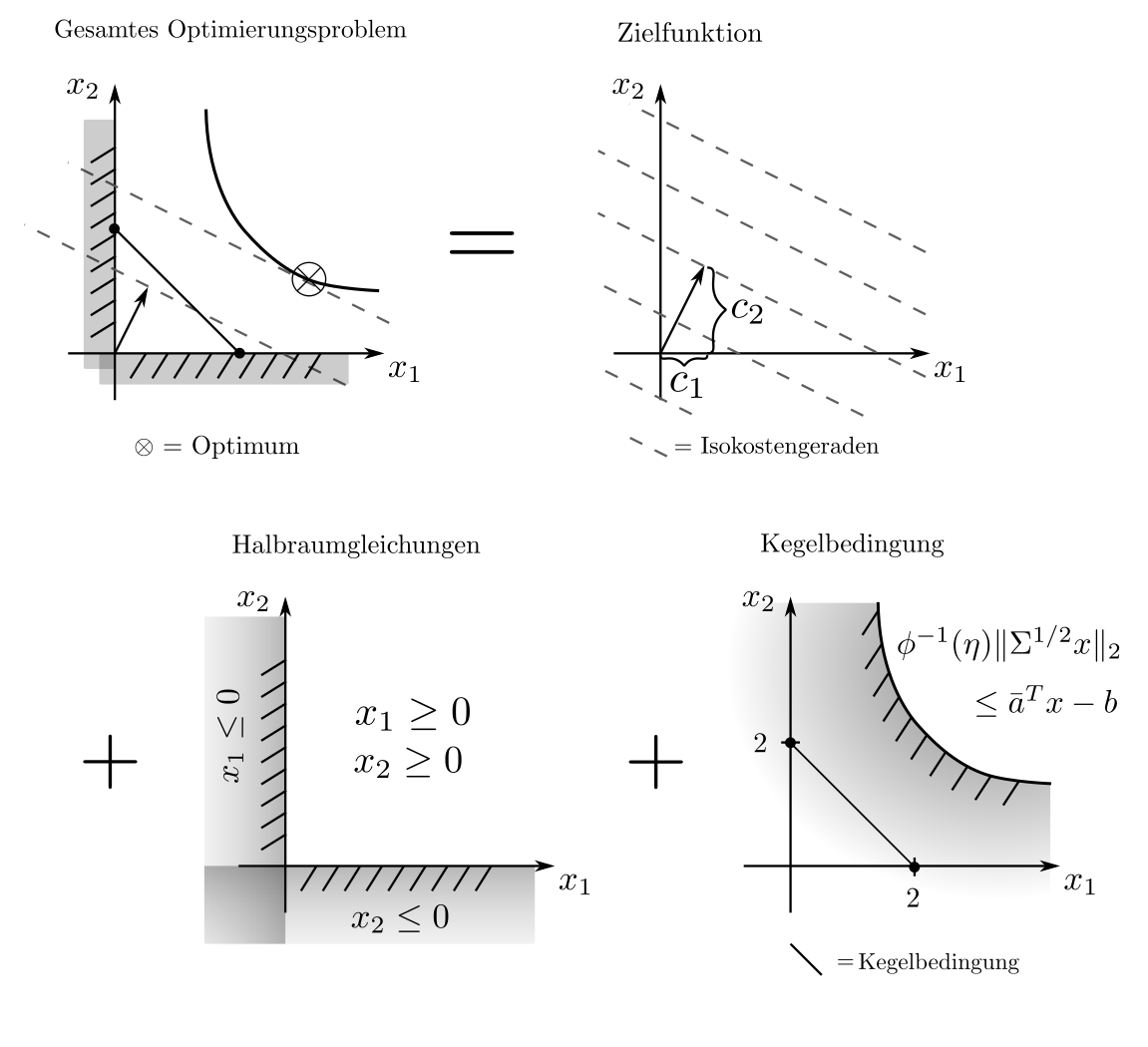
Geometrisches
Die Kegelbedingung \( \|\Sigma^{1/2} x\|_2 \le [\phi^{-1}(\eta]^{-1}(\bar{a}^Tx‑b)\) ist eine multivariate Generalisierung der klassischen Konfidenzintervalle. Während diese im eindimensionalen fall tatsächliche Intervalle sind, handelt es sich im zweidimensionen Fall um ellipsenartige Formen. Der Term \(\| \Sigma^{1/2} x\|_2\) ist die Standardabweichung der zufälligen Linearkombination \(a^Tx\) und damit ein Mass für die Streuung um den Erwartungswert \(\bar{a}^Tx\).
Beide Grössen werden zur Abschätzung der Wahrscheinlichkeit benötigt, dass der Anteil \(a^Tx\) fehlerfreier Produkte durch zufällige Schwankungen geringer ausfällt als der zu deckende Bedarf. Da \(\|\Sigma^{1/2} x\|_2\) und $\(a^Tx\) auf beiden Seiten der Gleichung vorkommen, ist eine Formulierung nur als SOCP und nicht als QCQP möglich.
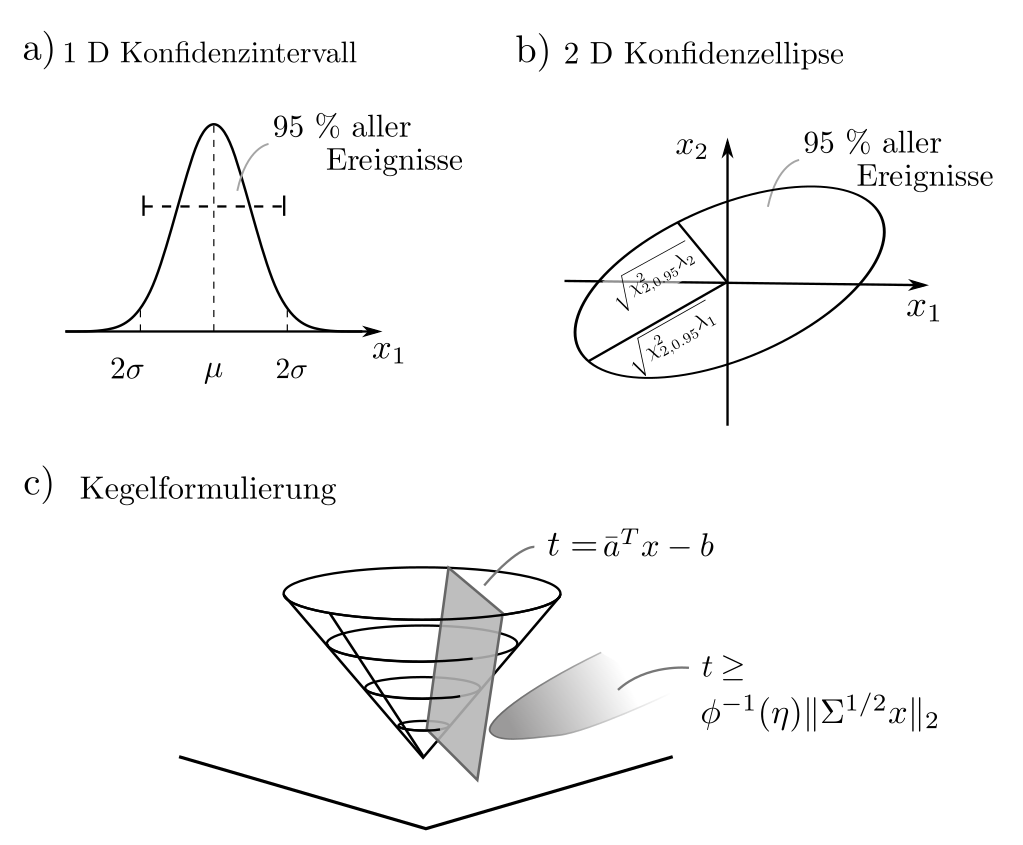
Anwendungen
Alle Beispiele für Anwendungen von LP sind auch Beispiele für Anwendungen von SOCP. Insbesondere lassen sich Probleme formulieren, die Vektorlängen und Ellipsoide beinhalten, worunter of die stochastischen Generalisierungen von LP und die Minimierung physikalisch motivierter quadratischer Energien fallen. Konkret sind das Portfolio Optimierungen, robustes LP, LP mit stochastischen Nebenbedingungen, optimale linear-quadratische Regelung kinematischer Systeme, physikalische Simulation, Parameterschätzung in Gausschen Modellen, robustes Least-Squares, Kalman Filterung, isotonische Regression, Antennedesign, Robotertrajektorienoptimierung, und Bildverarbeitung. Details sind hier zu finden.
Die Beispiele scheinen weniger praxisrelevant und intuitiv verständlich als bei LP. Das liegt jedoch daran, dass QP, QCQP, und SOCP das klassische LP um die Anwesenheit von Unsicherheit erweitern und neue Möglichkeiten für andere etablierte Techniken wie etwa das Least-Squares bereitstellen.
Lösungsverfahren
Da die zulässigen Mengen gekrümmt sind, ist eine Suche des Optimums durch Enumeration und Evaluation aller Eckpunkte nicht praktikabel. Lösungsansätze mit besonderem Geschwindigkeitsanspruch sind oft gradientenbasiert, da die Gradienten von quadratischen und linearen Termen einfach zu bestimmen sind. Es zählen dazu die Verfahren der konjugierten Gradienten, augmentierten Lagrangian und projizierten Gradienten [2, pp. 73, 116, 173]. Aufgrund der universellen Nutzbarkeit und zunehmender numerischer Performance finden sich vermehrt auch interior-point Methoden, welche Nebenbedingungen durch zusätzliche Strafterme ersetzen.
Praktisches
SOCP mit vielen zehntausend Variablen können heutzutage zuverlässig gelöst werden. Lösungsalgorithmen sind in Form von open source software verfügbar, z.B. der Splitting Conic Solver [3]. Es gibt durch die Nähe von QP und Finite Elemente Methoden auch Software spezifisch für Anwendungen in Baustatik und Maschinenbau [4]. Aufgrund der in Physik, Mechanik, und Statistik oft vorkommenden quadratischen Energieterme ist QP ein natürliches Instrument in diesen Disziplinen. Die richtige Form von QPs und QCQPs ist unter Umständen direkt aus einer Problemformulierung abzulesen; SOCPs sind typischerweise schwieriger zu interpretieren. Waren schon im LP nicht alle Einbettungen offensichtlich, so gilt dies hier in noch höherem Masse.
Code & Quellen
Beispielcode: Methods_socp.py in unserem Tutorialfolder
[1] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.
[2] Dostál, Zdenek. (2009) Optimal Quadratic Programming Algorithms: With Applications to Variational Inequalities. Berlin Heidelberg: Springer Science & Business Media.
[3] O’donoghue, B., Chu, E., Parikh, N., & Boyd, S. (2016). Conic Optimization via Operator Splitting and Homogeneous Self-Dual Embedding. Journal of Optimization Theory and Applications, 169(3), 1042–1068.
[4] Szabo, B. A., & Tsai C. (1973). The quadratic programming approach to the finite element method. International Journal for Numerical Methods in Engineering, 5(3), 375–381.
