Konvexität - Atlas optimization

Theorie: Konvexität

Definition

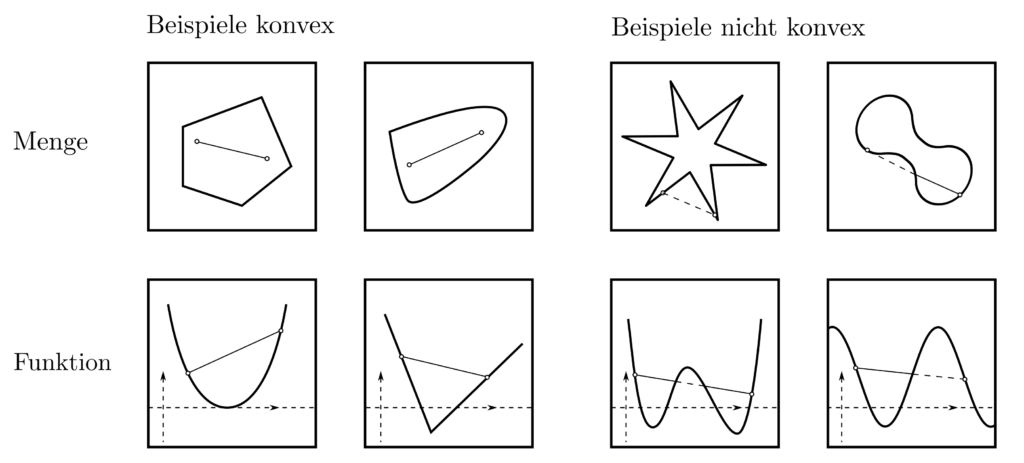
Eine Menge $D$ heisst konvex, wenn alle ihre Elemente durch gerade Linien verbunden werden können, die ganz in $D$ liegen. Konkret bedeutet es, dass für alle $x_1,x_2 \in D$ und $ y = \theta x_1 + (1-\theta)x_2 ~~~\theta \in [0,1]$ $y$ ein Element von $D$ ist.

Dabei sind sowohl $x_1, x_2$ als auch $y$ Vektoren beliebiger Dimension. Konvexe Mengen sind in dem Sinne einfache Objekte, als dass jeder Punkt von jedem anderen Punkt auf einfach Weise zu erreichen ist. Eine Funktion $f:D\rightarrow \mathbb{R}$ heisst konvex, wenn $D$ konvex ist und jede lineare Approximation an $f$ komplett über $f$ liegt. Formell gesehen bedeutet der letzte Punkte, dass für alle $x_1, x_2 \in D$ und alle $\theta \in [0,1]$ gilt:

$$ \theta f(x_1) + (1-\theta)f(x_2) \ge f(\theta x_1 + (1-\theta) x_2) $$

Dass der Wert eines konvexen $f$ an einer Stelle $x$ immer unter dem Mittelwert seiner Nahbarn liegt, impliziert die Abwesenheit hügelartiger Formen in der Funktionslandschaft von $f$ und eine stets nach oben gerichtete (=positive) Krümmung. Eine umfassende Quelle betreffen Konvexität von Mengen und Funktionen ist [1, pp. 23–90].

Relevanz

Konvexe Menge und konvexe Funktionen sind Garanten für eindeutige und praktisch durchführbare Minimierbarkeit. Dies ist etwas besonderes, denn Optimierungsprobleme sind typischerweise unlösbar [2, p.4]. Wie in der obigen Abbildung zu erkennen, impliziert die Existenz mehrerer Minima, dass eine Funktion nicht konvex ist. Als konverse Aussage folgt, dass bei konvexem $f$ nur ein lokales Minimum existiert.

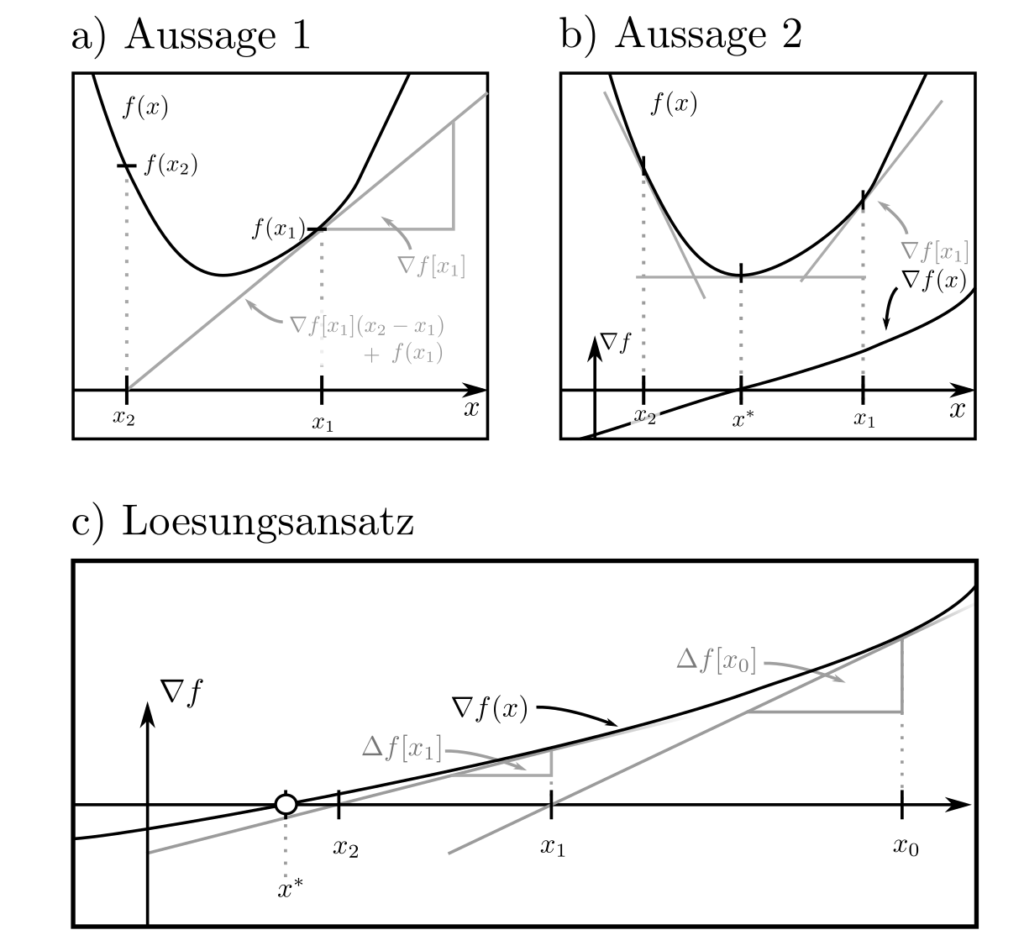
Zusätzlich können dank der Konvexität von $f$ von lokalen Eigenschaften auf globale Eingenschaften geschlossen werden. Unter der Annahme von Differenzierbarkeit von $f$ gelten die beiden Aussagen:

$f(x_2) \ge f(x_1) + \nabla f(x_1)^T[x_1-x_1]$
$\Delta f(x)\succeq 0$

für alle $x_1$ und $x_2$ wobei $\nabla f$ der Gradient (=Vektor erster Ableitungen) und $ \Delta f$ die Hesse-Matrix (=Matrix zweiter Ableitungen) von $f$ sind. Eine konvexe differenzierbare Funktion ist gemäss den obigen Aussagen immer nichtnegativ gekrümmt und wird nach unten hin durch lineare Approximation beschränkt. Konsequenterweise befindet sich das globale Minimum an derjenigen Stelle $x^*$, für die $\nabla f(x)=0$ gilt. Dies folgt aus $$f(x_1)\ge f(x^*) + \underbrace{\nabla f(x^*)[x^*-x_2]}_{=0} \ge f(x^*)$$.

Lösungsansatz

Die Suche nach Nullstellen von $\nabla f$ führt direkt auf das in der obigen Abbildung rechts illustrierte Verfahren: Man starte an einem beliebigen Punkt $x_0$, verwende den Wert $\nabla f(x_0)$ des Gradienten und dessen Änderungsrate $\Delta f (x_0)$, um die Nullstelle zu schätzen. Mit dem Schätzer $x_1$ für die Nullstelle wiederhole die Prozedur, bis die tatsächliche Nullstelle $x^*$ ausfindig gemacht wurde.

Aus $\nabla f(x_0) + \Delta f[x_1 ‑x_0]\stackrel{!}{=}0$ ergibt sich als Lösung für die aus $x_0$ abgeleiteten Nullstellenschätzer die Folge $$ x_{k+1} = x_K +\Delta f^{-1}(x_k) \nabla f(x_k) ~~~~k=0,1, …$$

Dieses Verfahren ist auch bekannt als das Newton Verfahren. Aufgrund der positiven Krümmung weist jeder Punkt $x_{k+1}$ geringeren Funktionswert $f(x_{k+1})$ auf als sein Vorgänger $x_k$ und das Verfahren terminiert beim Optimum $x^*$ [1, p. 484]. Es kann mit Modifikationen auch für Optimierungsprobleme mit Nebenbedingungen angewendet werden. Mehr dazu hier.

Beispiele

Viele wichtige Funktionen sind konvex und können damit effizient optimiert werden. Die Beispiele der folgenden nicht exklusiven Liste sind [1, pp. 71–73] entnommen.

Name	Funktion	Definitionsmenge	Anwendung Modellierung
Exponentialfunktion	$e^{ax}$	$x\in \mathbb{R}, a \in \mathbb{R}$	Wachstums- und Zufallsprozesse
Neg. Logarithmus	$-\log x$	$x > 0$	Wahrscheinlichkeitsverteilungen
Lineares Funktional	$c^T x$	$x\in \mathbb{R}^n, c \in \mathbb{R}^n$	Kombination von Effekten
Norm	$\\|x\\|_p$	$x \in \mathbb{R}^n, p \ge 1$	Diskrepanzen und Entfernungen
Neg. Entropie	$-\sum_{k=1}^n p(x_k)\log p(x_k) $	$p(x_k)> 0$	Vergleich Wahrscheinlichkeitsverteilungen
Neg. Geom. Mittel	$ — \left(\Pi_{k=1}^n x_k\right)^{1/n}$	$ x\in \mathbb{R}^n, x_k >0$	Wachstumsprozesse und Indikatorgrössen
Maximum	$\max (x_1, …, x_n)$	$ x\in \mathbb{R}^n$	Überproportionale Einfüsse
Softmax	$\log \left( \sum_{k=1}^n e^{x_k}\right)$	$ x\in \mathbb{R}^n$	Machine Learning
Neg. Logdet	$- \log \det X$	$X$ positiv definit	Kovarianzmatrizen und Energien
Eigenwertsumme	$ \sum_{k=1}^n \lambda_k(X)$	$X$ positiv semidefinit	Unsicherheiten und Verteilungseigenschaften
Matrixbruch	$x^YP^{-1}x$	$ x\in \mathbb{R}^n, P$ positiv semidefinit	Normalverteilungen und anisotrope Entfernungen

Konstruktionsregeln

Die obigen Beispiele können kombiniert werden, um neue, ausdrucksfähigere konvexe Funktionen zu generieren. Positiv gewichtete Linearkombinationen $w_1f_1(x)+w_2f_2(x)$ konvexer Funktionen $f_1(x), f_2(x)$ sind konvex; selbiges gilt für das Maximum $\max( f_1(x),f_2(x))$ oder die Komposition mit einer linearen Transformation zu $f_1(Ax+b)$. Moderne Modellierungsframeworks wie CVXPY [3] machen sich diese Zusammenhänge zu nutze. Ausgehend von nachweisbar konvexen Beispielfunktionen und konvexitätserhaltenden Kompositionsregeln können of selbst kompliziert erscheinende Funktionen auf Verknüpfungen elementarer konvexer Funktionen zurückgeführt und anschliessen gelöst werden [4].

Quellen

[1] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.

[2] Nesterov, Y. (2013). Introductory Lectures on Convex Optimization: A Basic Course. Berlin Heidelberg: Springer Science & Business Media.

[3] Diamond S., & Boyd S., (2016). CVXPY: A Python-embedded modeling language for convex optimization. Journal of Machine Learning Research, 17(83), 1–5.