Theorie: Stochastizität
Modelle und Unsicherheit

Unsicherheit ist ein essentieller Bestandteil von Modellen zur Abbildung von Echtweltphänomenen. Sie kann verschiedene Ursachen haben.
- Das Modell involviert Phänomene zufälliger Natur wie etwa Kernzerfall, Bauteilversagen, oder Aktienkurse
- Das Modell beinhaltet deterministische aber unbekannte Grössen wie etwa die Länge einer unzureichend genau gemessenen Strecke oder den noch unveröffentlichten Preis eines Produktes.
- Das Modell ist bewusst unvollständig und die Abweichungen zwischen Modellverhalten und Realität werden als Unsicherheit angerechnet; etwa bei kontinuumsmechanischen Problemen oder Rückkoplungseffekten in komplexen Systemen.
Zufallsvariablen
Dabei nehmen Zufallsvariablen und deren Wahrscheinlichkeitsverteilungen eine zentrale Stellung ein. Eine Zufallsvariable \(X^{\cdot}\) ist eine Abbildung $$X^{\cdot}:\Omega \ni \omega \mapsto X^{\omega}\in \mathbb{R}$$ welche dem Resultat eines Experimentes eine Zahl zuordnet [1, p. 46]. Das Experiment kan z.B. das Werfen eines Würfels, das Resultat die obenliegende Würfelfläche sein und die Zufallsvariable bildet dieses Resultat ab auf die Augenzahl. Bevor ein Würfelwurf tatsächlich stattfindet, ist das Resultat des Experimentes nicht bekannt, kann aber hinsichtlich der erwarteten Häufigkeiten möglicher Augenzahlen beschrieben werden. Diese relativen Häufigkeiten werden Wahrscheinlichkeiten genannt; die Zuweisung der Wahrscheinlichkeiten zu den unterschiedlichen numerischen Werten heisst Wahrscheinlichkeitsverteilung.
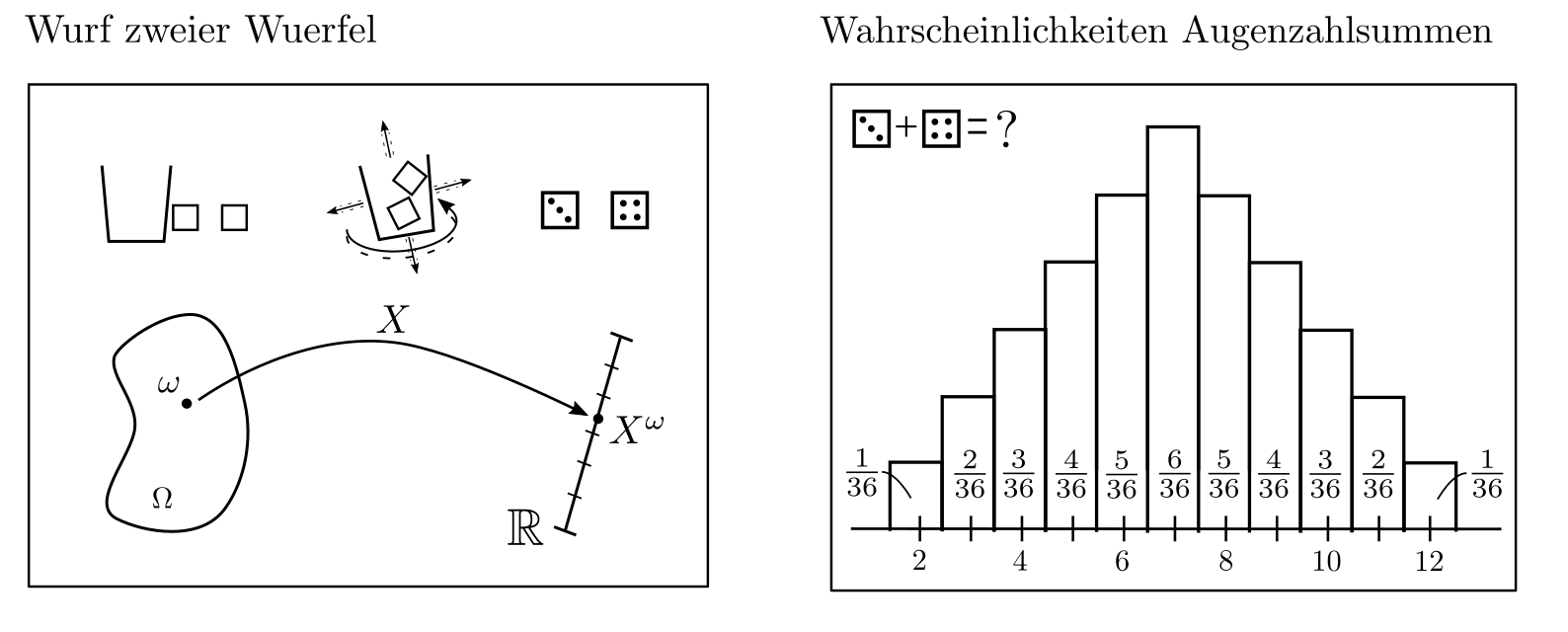
Relevanz
Tritt in einem Optimierungsproblem die Zufallsvariable \(X^{\cdot}\) auf, so muss die Gesamtheit aller möglichen von \(X^{\cdot}\) angenommenen Werte und deren individuelle Wahrscheinlichkeiten berücksichtigt werden. Dies macht Optimierungsprobleme schwieriger zu interpretieren und für eine Lösung müssen Entscheidungen getroffen werden, welcher Aspekt der Wahrscheinlichkeitsverteilung der nun ebenfalls zufälligen Zielfunktion zu optimieren ist.
Ist die Zielfunktion z.B. gegeben durch Kosten \(c^Tx\) mit Optimierungsvariable \(x\in \mathbb{R}^n\) und Zufallsvariablen \([c_1^{\cdot}, …, c_n^{\cdot}]=c^T\), so mag es sinnvoll sein, Erwartungswert, Schwankungsbreite, Maximalwerte, oder Quantile der Kosten zu minimieren. Je nach Zielvorstellung ührt dies zu LP, SDP, oder stochastischen Programmen.
Typische Wahrscheinlichkeits-verteilungen
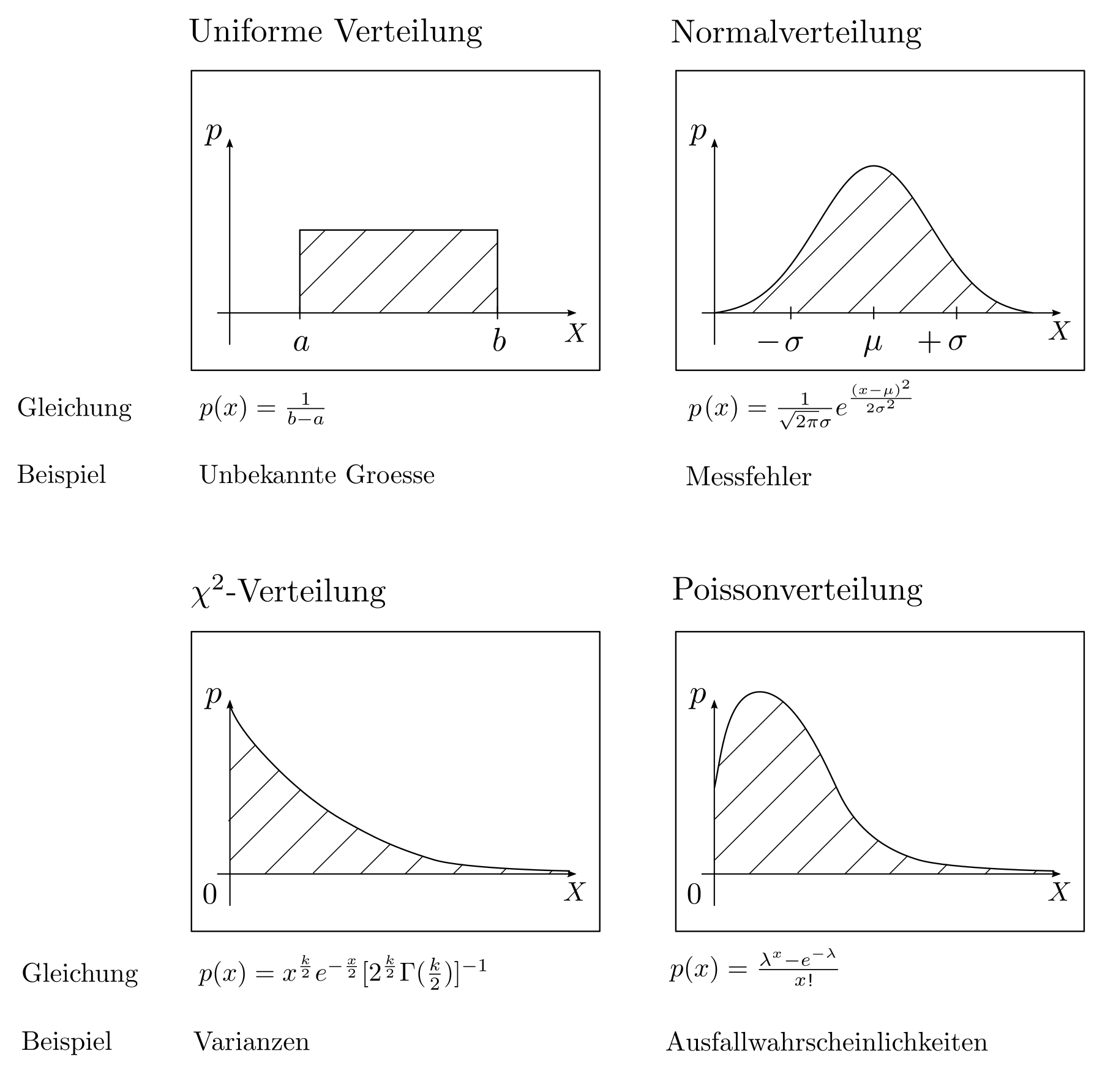
Welche Wahrscheinlichkeitsverteilung am geeignetsten ist zur Modellierung eines Zufallsaspektes hängt von den genauen Hintergründen ab. Uniforme Verteilungen symbolisieren komplettes Unwissen während Normalverteilungen gute Approximationen sind für sich aus vielen unabhängigen kleinen Fehlern zusammensetzende Zufallseffekte. Die \(\chi^2\)-Verteilung quantifiziert Unsicherheiten im Zusammenhang mit Längen und Entfernungen und die Poisson Verteilung kann zur Beschreibung von Ausfallwahrscheinlichkeiten herangezogen werden. Diverse massgeschneiderte Wahrscheinlichkeitsverteilungen und deren Anwendungen sind z.B. in [2, pp. 828–828] zu finden.
Stochastische Prozesse
Besonders praxisrelevant sind multivariate Wahrscheinlichkeitsverteilungen. Sie quantifizieren die Eintrittswahrscheinlichkeiten von stochastischen Prozessen: Sammlungen von untereinander korrelierten Zufallsvariablen, die Zeitpunkten, Orten oder allgemeiner beliebigen Indexmenge zugeordnet werden [1, p. 190]. Stochastische Prozesse können zur Beschreibung von durch Zufall beeinflussten Phänomenen in Raum oder Zeit eingesetzt werden und selbst die simplen multivariaten Normalverteilungen decken eine grosse Bandbreite an potentiell zu modellierendem Verhalten ab [3, pp. 79–94].
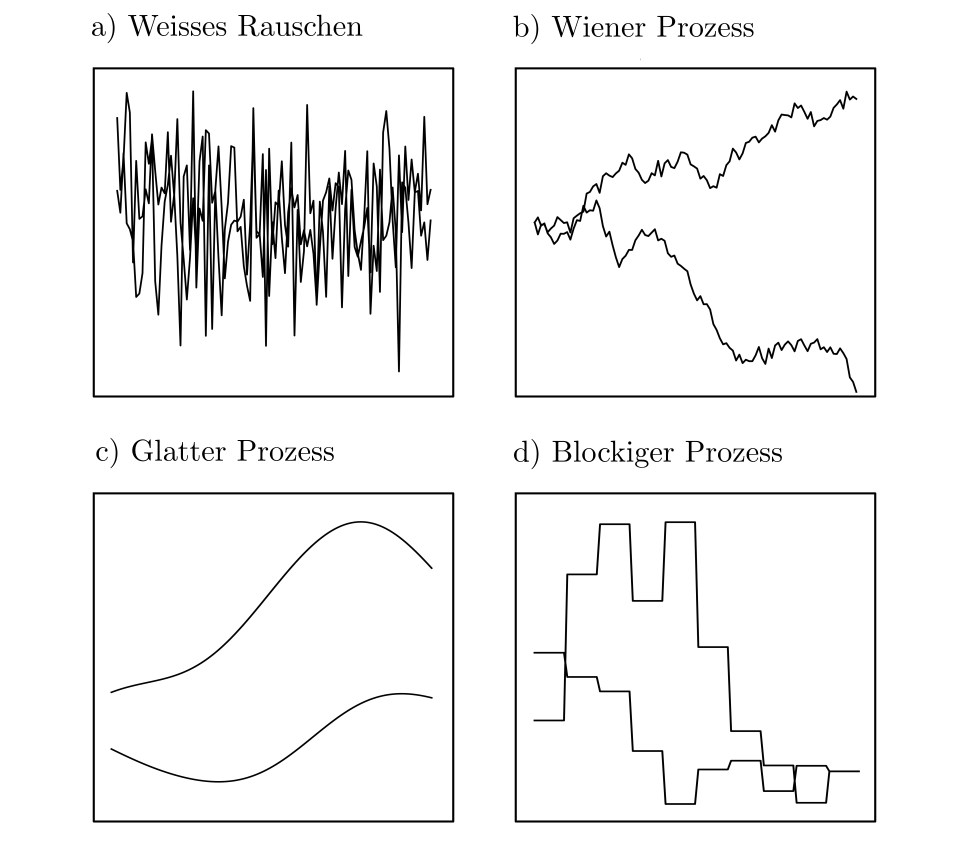
An den Abbildungen ist erichtlich, dass selbst zufällig generierte Funktionen funktionale Zusammenhänge aufweisen können. Prinzipiell ist die Annahme von Stochastizität selten hinderlich, da stochastische Modelle die deterministischen modelle als Teilmenge inkludieren.
Beispielanwendung
Sei \(X^{\cdot}_{\cdot}:T\times \Omega \ni (t,\omega)\mapsto X^{\omega}_{t} \in \mathbb{R}\) ein stochastischer Prozess; d.h. eine Folge von Zufallsvariablen indiziert durch die Zufallsvariable \(t\in T\). Ist der Prozess nur zu einigen Zeitpunkten beobachtet worden und soll für alle anderen Zeitpunkte aus den Beobachtungen geschätzt werden, so kann dies als Optimierungsproblem formuliert werden. Unter der Annahme bekannter Wahrscheinlichkeitsverteilung und damit bekannter Kovarianzen ist der beste Schätzer \(\hat{X}_{t_0}\) für den Wert an der Stelle \(t_0\) basierend auf den Beobachtungen \(X_{t_1}, …, X_{t_n}\) gegeben als
$$\hat{X}_{t_0} = \sum_{k=1}^n \lambda_k X_{t_k}.$$
Dabei ist \([\lambda_1, … ‚\lambda_n]=\lambda\) Lösung des quadratischen Programmes
$$\begin{align} \min_{\lambda} ~~~&\lambda^TC\lambda‑2\lambda^T c + \sigma_{00} \\
\text{s.t.} ~~~&\sum_{k=1}^n \lambda_k=1 \end{align}$$
mit \(c\in \mathbb{R}^n, ©_k=\text{ Kovarianz}(X_{t_0},X_{t_j})\), \(C\in \mathbb{R}^{n\times n}, ©_{kl}= \text{ Kovarianz}(X_{t_k},X_{t_l})\), und \(\sigma_{00} = \text{ Kovarianz}(X_{t_0},X_{t_0})\). Dieses Problem kann leicht algorithmisch oder per hand gelöst werden und führt auf das in der Geostatistik häufig eingesetzte Verfahren namens Kriging [4, pp. 163–164]. Der Wert des Minimierungsproblemes ist die Varianz des Schätzfehlers.
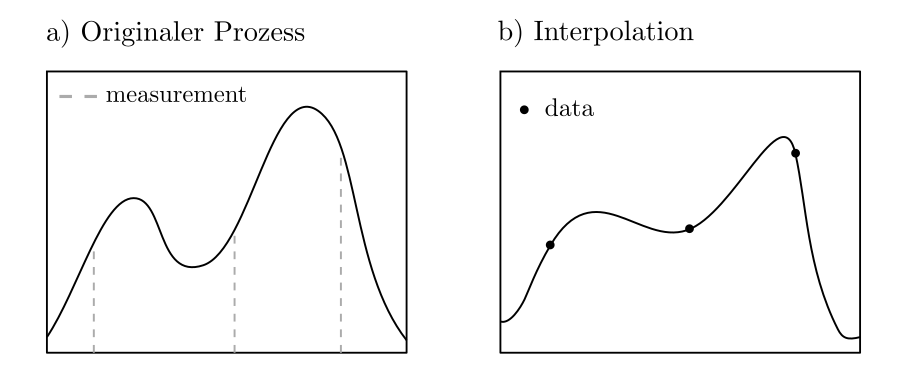
Praktisches
Unsicherheiten sind Teil aller Echtweltphänomene und müssen auch in den Optimierungsproblemen entsprechend repräsentiert werden. Dazu müssen angemessene und auf das Phänomen zugeschnittene Wahrscheinlichkeitsverteilungen ausgewählt werden. Da es in den allermeisten Fällen um mehr geht als nur eine zufällige Grösse, werden stochastische Prozesse zur Modellierung eingesetzt. Diese verfügen über hochdimensionale Wahrscheinlichkeitsverteilungen udn müssen so ins Optimierungsproblem eingebunden werden, dass sinnvolle Lösungen abgeleitete werden können. Dies geht gut mit multivariat normalverteilten und uniform verteilten Daten aber ist herausfordernf für weniger erschöpfend untersuchte Wahrscheinlichkeitesverteilungen.
Code & Quellen
Beispielcode: Theory_stochastic_processes.py in unserem Tutorialfolder
[1] Melsa, J. L., & Sage, A. P. (2013). An Introduction to Probability and Stochastic Processes. New York: Courier Corporation.
[2] Bronstein, I. N., Mühlig, H., Musiol, G. & Semendjajew, A. K. (2013). Taschenbuch der Mathematik. Haan-Gruiten: Verlag Europa-Lehrmittel
[3] Rasmussen, C. E., & Williams, C. K. (2005). Gaussian Processes for Machine Learning. Cambridge: MIT Press.
[4] Chilès, J. P., & Delfiner, P. (2009). Geostatistics: Modeling Spatial Uncertainty. New York: John Wiley & Sons.
